Definition, Equation Formula, Solved Example Problems, Exercise | Analytical Geometry | Mathematics - Pair of Straight Lines | 11th Mathematics : UNIT 6 : Two Dimensional Analytical Geometry
Chapter: 11th Mathematics : UNIT 6 : Two Dimensional Analytical Geometry
Pair of Straight Lines
Pair of Straight Lines
The equations of two or more lines can be expressed together by an equation of degree higher than one. As we see that a linear equation in x and y represents a straight line, the product of two linear equations represent two straight lines, that is a pair of straight lines. Hence we study pair of straight lines as a quadratic equations in x and y.
Let L1 ≡ a1x + b1y + c1 = 0 and L2 ≡ a2x + b2y + c2 = 0, be separate equations of two straight lines. If P (x1, y1) is a point on L1, then it satisfies the equaiton L1 = 0. Similarly, if P (x1, y1) is on L2 then L2 = 0. If P (x1, y1) lies either on L1 = 0 or L2 = 0, then P (x1, y1) satisfies the equation (L1 ) (L2) = 0, and no other point satisfies L1 · L2 = 0. Therefore the equation L1 · L2 = 0 represents the pair of straight lines L1 = 0 and L2 = 0.

1. Pair of Lines Passing through the Origin
We first consider a simple case. Both the lines in this pair pass through the origin. Thus, their equations can be written as
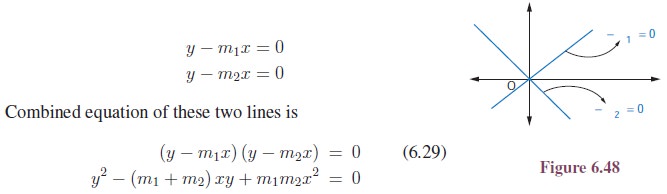
The above equation suggests that the general equation of a pair of straight lines passing through the origin with slopes m1 and m2, ax2 + 2hxy + by2 = 0 is a homogenous equation of degree two, implying that the degree of each term is 2.



2. Angle between Pair of Straight Lines

As a consequence of this formula, we can conclude that
· The lines are real and distinct, if m1 and m2 are real and distinct, that is if h2 − ab > 0
· The lines are real and coincident, if m1 and m2 are real and equal, that is if h2 − ab = 0
· The lines are not real (imaginary), if m1 and m2 are not real, that is if h2 − ab < 0
Also, we see that the lines represented by (6.30), are parallel (since both pass through the origin, the lines are coincident lines) if tan θ = 0, that is h2 − ab = 0, and perpendicular if cot θ = 0 that is a + b = 0


3. Equation of the bisectors of the angle between the lines
ax2 + 2hxy + by2 = 0 Let the equations of the two straight lines be y − m1x = 0 and y − m2x = 0
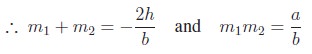
We know that the equation of bisectors is the locus of points from which the perpendicular drawn to the two straight lines are equal.
Let P (p, q) be any point on the locus of bisectors.
The perpendiculars from P (p, q) to the line y − m1x = 0 is equal to the perpendicular from P (p, q) to y − m2x = 0
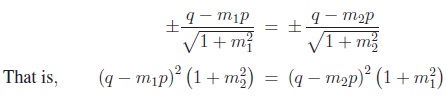
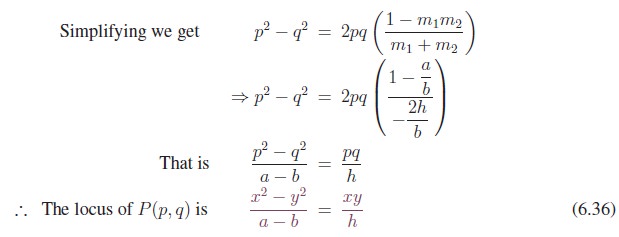


4. General form of Pair of Straight Lines
Consider the equations of two arbitrary lines l1x + m1y + n1 = 0 and l2x + m2y + n2 = 0 The combined equation of the two lines is
(l1x + m1y + n1) (l2x + m2y + n2) = 0
If we multiply the above two factors together, we get a more general equation to a pair of straight lines has the form
ax2 + 2hxy + by2 + 2gx + 2f y + c = 0 ......................6.40
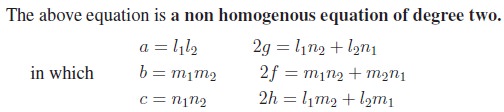
An equation of the form (6.40) will always represent a pair of straight lines, provided it must able to be factorized into two linear factors of the form l1x + m1y + n1 = 0 and l2x + m2y + n2 = 0.
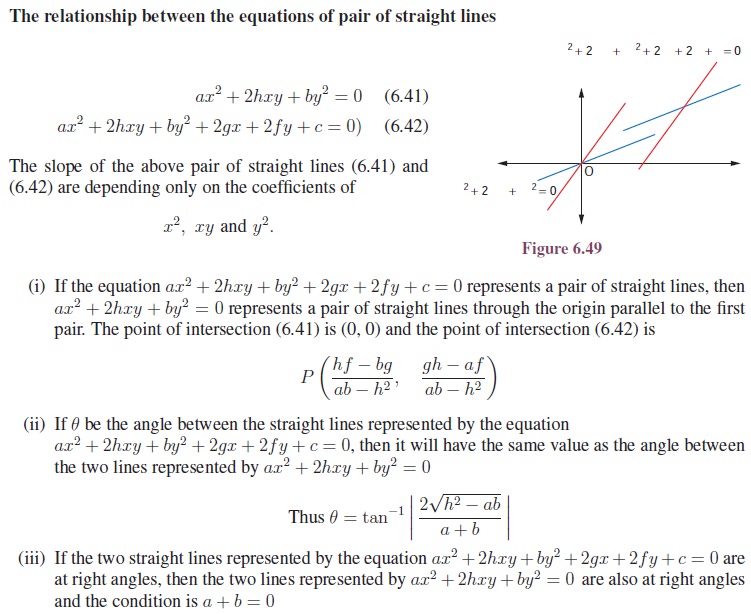
Condition that the general second degree equation ax2 + 2hxy + by2 + 2gx + 2f y + c = 0 should represent a pair of straight lines
Let us rearrange the equation of the pair of straight lines ax2 + 2hxy + by2 + 2gx + 2f y + c = 0 as a quadratic in x, we have
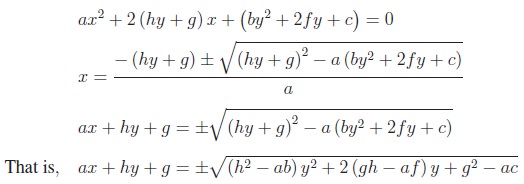
Since each of the above equations represents a straight line, they must be of the first degree in x and y. Therefore the expression under the radical sign should be a perfect square and the condition for this is



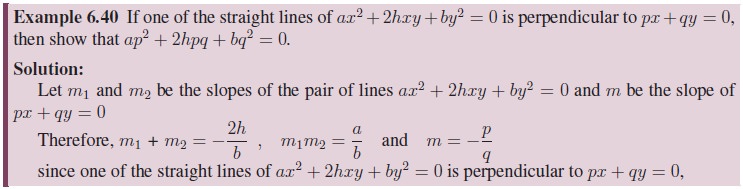



Related Topics