Locus of a point

Locus of a point

It is important to understand that a point is not a thing, but a place. We indicate the position of a point by placing a dot. In plane analytical geometry, points are defined as ordered pairs of real numbers, say, (x, y) with reference to the coordinate system.

Generally, a horizontal line is called the x-axis; and the line vertical to the x-axis is called the y-axis. Intersection of these two axes is called the origin. Any point P in the plane can be located by a unique ordered pair of numbers(x, y) where x gives the distance between the point P and the y-axis and y denote the distance between the point P and the x-axis. Note that if x is negative it lies left of y − axis, similarly if y is negative it lies below the x-axis. In applications, often letters other than x and y are used, and different scales are chosen in the horizontal and vertical directions.

The following illustrations shows some cases of loci and its different uses.

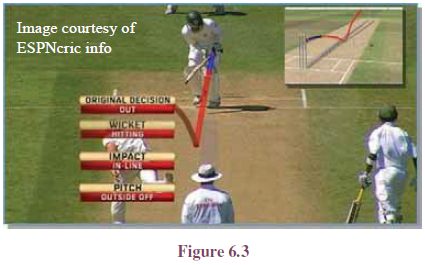
Illustration 6.1: In cricket, when a ball is bowled by a bowler, the path traced out by the ball is the locus of the ball. Whenever there is dispute between batsmen and the fielders for leg before wicket (LBW) decisions, the locus of the ball solves the crises, raised by the players for review, through the third umpire. The likely path of the ball can be projected forward, through the batsman’s legs, to see whether it would have hit the stumps or not. Consultation of the third umpire, for conventional slow motion or Hawk Eye, the probable decision will be taken. This method is currently sanctioned in international cricket.

Illustration 6.2: Suppose P be a point on the rim (circumference) of a circular wheel. When the circle is rolling without slipping along a straight line, the locus of the point P on the rim is shown in figure. The path traced out by the point P is known as cycloid. (Try yourself by taking a point inside the circle.

Illustration 6.3: A missile is launched from the army ship to attack and another from the land to intercept it. The loci of the missiles are shown in figure.

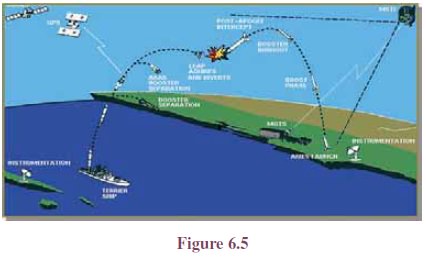
Locus of missiles play a vital role in many wars. During the Gulf War (2 Aug1990-28 Feb 1991), Iraq attacked Israeli cities with Scud missiles. To defend from Scud attack, Israel used Patriot missiles to shoot down enemy missiles. To launch a satellite or space shuttle successfully, the determination of path plays an crucial role in space research.

An equation in the two variables x and y will ordinarily be satisfied by infinitely many pair of real value of x and y. Every such pair is called a real solution of the equation. Each real solution of the equation will have its graph. The collection of all these graphs is called the locus of the given equation.

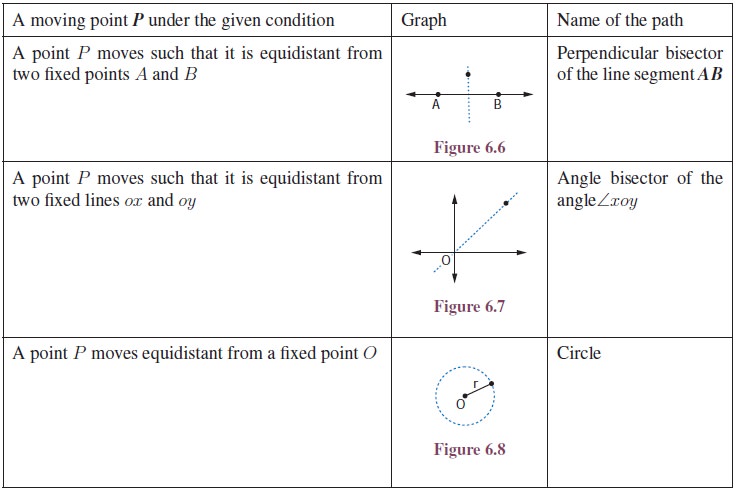
The following table shows some important loci in mathematics

Now let us discuss the ways of finding the locus of the points. The equation of the locus is the relation that exists between the coordinates of all the points strictly lying on the path.

Procedure for finding the equation of the locus of a point

i.            If we are finding the equation of the locus of a point P, assign coordinates, say (h, k) to P

ii.            Express the given conditions as equations in terms of the known quantities and unknown parameters.

iii.            Eliminate the parameters, so that the resulting equation contains only h, k and known quantities.

iv.            Replace h by x, and k by y, in the resulting equation. The resulting equation is the equation of the locus of point P.