Exercise 4.4

Exercise 4.4

Miscellaneous Practice Problems

1. Find the type of lines marked in thick lines (Parallel, intersecting or perpendicular).

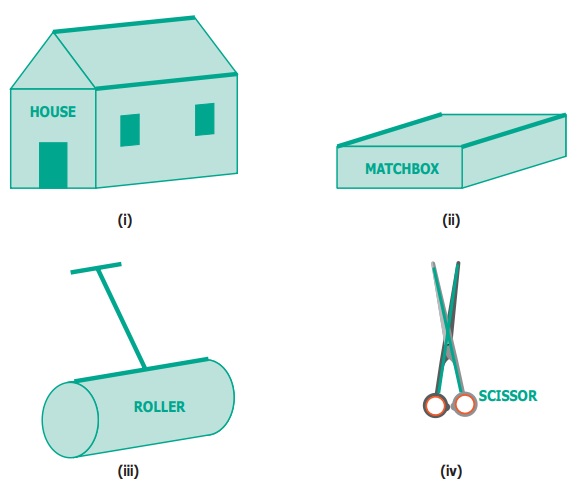
Answer: (i) Parallel lines

(ii) Parallel lines

(iii) Parallel & Perpendicular lines

(iv) Intersecting lines.

2. Find the parallel and intersecting line segments in the picture given below.

3. Name the following angles as shown in the figure.

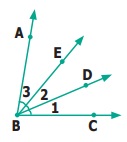
(i) ∠1 =

(ii) ∠2 =

(iii) ∠3 =

(iv) ∠1 + ∠2 =

(v) ∠2 + ∠3 =

(vi) ∠1 + ∠2 + ∠3 =

Answer:

(i) ∠1 = ∠CBD (or) ∠DBC

(ii) ∠2 = ∠DBE (or) ∠EBD

(iii) ∠3 = ∠EBA (or) ∠ABE

(iv) ∠1 + ∠2 = ∠CBE (or) ∠EBC

(v) ∠2 + ∠3 = ∠DBA (or) ∠ABD

(vi) ∠1 + ∠2 + ∠3 = ∠ABC (or) ∠CBA

4. Measure the angles of the given figures using protractor and identify the type of angle as acute, obtuse, right or straight.

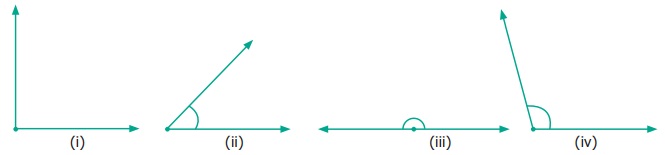
Answer:

(i) Right angle

(ii) Acute angle

(ii) Straight line

(iv) Obtuse angle 

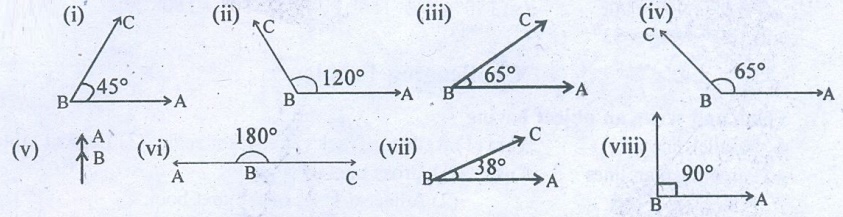
5. Draw the following angles using the protractor.

(i) 45º

(ii) 120º

(iii) 65º

(iv) 135º

(v) 0º

(vi) 180º

(vii) 38º

(viii) 90º

6. From the figures given below, classify the following pairs of angles into complementary and non complementary.

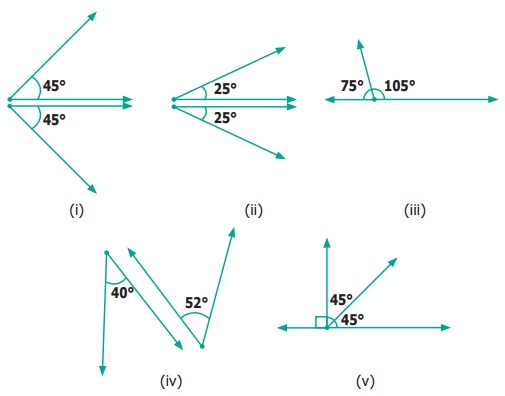
Answer: 

Complementary – ( i) & (v)

Non−complementary − (ii), (iii) & (iv) 

7. From the figures given below, classify the following pairs of angles into supplementary and non supplementary.

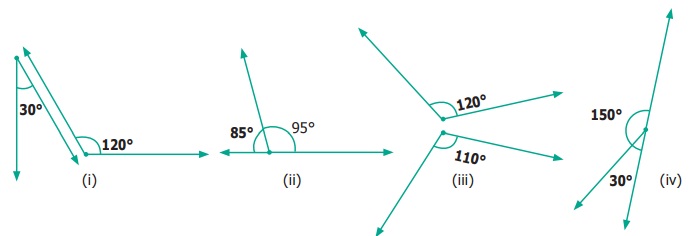
Answer:

Supplementary − (ii) & (iv)

Non−Supplementary − (i), (iii)

8. From the figure

(i) name a pair of complementary angles

(ii) name a pair of supplementary angles

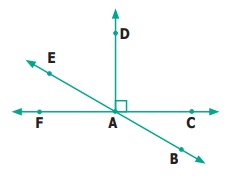
Answer:

(i) Complementary angles

∠FAE & ∠EAD

(ii) Supplementary angles

(a) ∠FAD & ∠DAC

(b) ∠BAF & ∠FAE

(c) ∠EAD & ∠DAB

(d) ∠BAC & ∠CAE 

9. Find the complementary angle of

(i) 30º

(ii) 26º

iii) 85º

(iv) 0º

(v) 90º

Solution: Complementary angle (90°− θ)

(i) 90° − 30° = 60°

(ii) 90° − 35° = 65°

(iii) 90° − 85° = 5°

(iv) 90° − 0° = 90°

(v) 90° − 90° = 0° 

10. Find the supplementary angle of

(i) 70º

(ii) 35º

(iii) 165º

(iv) 90º

(v) 0º

(vi) 180º

(vii) 95º

Solution: Supplementary angle (180° − θ°)

(i) 180° − 70° = 110°

(ii) 180° − 35° = 145°

(iii) 180° − 165° = 15°

(iv) 180° − 90° = 90°

(v) 180°− 0° = 180°

(vi) 180° − 180° = 0°

(vii) 180° − 95° = 85°

Challenging Problems

11. Think and write an object having

● Parallel lines (1) __________ (2) __________ (3) __________

● Perpendicular lines (1) __________ (2) __________ (3) __________

● Intersecting lines (1) __________ (2) __________ (3) __________

• Parallel lines

Answer: (1) Railway Track (2) edgesof scale (3) Legs of table

• Perpendicular lines

Answer:

(1) Cross bars of windows

(2) Adjacent sides of the text book

(3) Adjacent sides of Black board

• Intersecting lines

Answer: (1) Ladder (2) Blades of scissor (3) Cross bars of windows

12. Which angle is equal to twice its complement?

Answer: 60°

13. Which angle is equal to two-third of its supplement?

Answer: 72°

14. Given two angles are supplementary and one angle is 20º more than other. Find the two angles.

Answer: The two angles are 80° & 100°

15. Two complementary angles are in ratio 7:2. Find the angles.

Answer: Two angles are 70° & 20°

16. Two supplementary angles are in ratio 5:4. Find the angles.

Answer: The angles are 100° & 80°

Answers:

Exercise 4.4

1) i) Parallel lines

ii) Parallel lines

iii) Parallel and Perpendicular lines

iv) Intersecting lines

2) Parallel lines

3) i) ∠1 = ∠CBD or ∠DBC

ii) ∠2 = ∠DBE or ∠EBD

iii) ∠3 = ∠ABE or ∠EBA

iv) ∠1+∠2 = ∠CBE or ∠EBC

v) ∠2 + ∠3 = ∠ABD or ∠DBA

vi) ∠1 + ∠2 + ∠3 = ∠ABC or ∠CBA

4) i) right angle ii) acute angle iii) straight angle iv) obtuse angle

6) (i) and (v) are complementary angles (ii), iii) and iv) are non-complementary angles

7) ii) and iv) are supplementary

     i) and iii) are not supplementary

8) i) ∠ FAE; ∠EAD

ii) ∠FAD; ∠DAC

 ∠BAC; ∠CAE

 ∠ FAB; ∠BAC

 ∠ FAB; ∠FAE

9) i) 60˚ ii) 64˚ iii) 5˚ iv) 90˚ v) 0˚

10) i) 110˚ ii) 145˚ iii) 15˚ iv) 90˚ v) 180˚ vi) 0˚ vii) 85˚

11) i) Legs of the table, railway track, edges of the scale

ii) Adjacent sides of a Board, Cross bars of windows, Adjacent sides of the textbook

iii) Cross bars of windows, Ladder, blades of a scissor.

12) 60˚ is twice its complement.

13) 72˚

14) The two angles are 80˚ and 100˚

15) Two angles are 70˚ and 20˚.

16) The angles are 100˚ and 80˚.

EUCLID

(325 BC – 265 BC)

He was a Greek Mathematician who founded the plane geomety through his postulates in a set of 13 books called "ELEMENTS". His work “ELEMENTS” influenced the whole world’s understanding of geometry for generations.