Angles

Angles

Can we find a way to describe all these shapes? (shown in fig. 4.20)

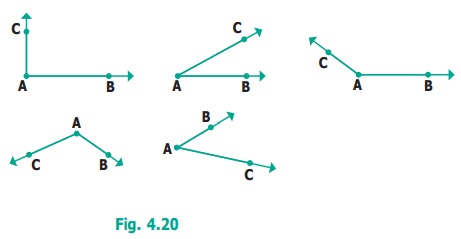
How would you describe whether a ray (or line segment) is vertical or slanting with respect to another ray (or line segment)?

Note

We can do the same with two line segments also. See the figures given below.

Carrom board involves many geometric concepts like line segments and angles. When the striker hits the coin, the coin moves in a straight line. When the striker or coins hit the board end they make angles with the board while returning.

When two rays or line segments meet at their end points, they form an angle at that point.

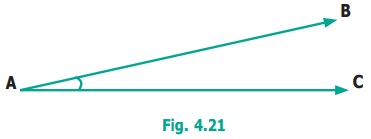
In the Fig.4.21 rays  are the sides and ‘A’ is the vertex which is the meeting point of both the line segments.

1. Naming Angles

We name the angle as shown in the Fig.4.22 below.

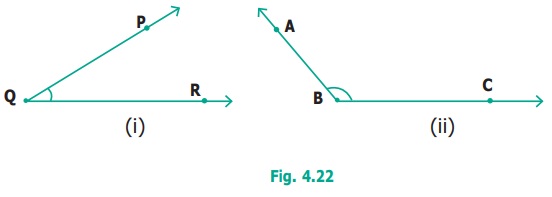
Fig 4.22(i) shows ∠PQR; ,  are its sides. 'P' is on ; 'R' is on .

Fig 4.22(ii) shows ∠ABC; ,  are its sides. 'A' is on ; 'C' is on .

We name the angles in fig. 4.22 (i) as ∠Q or ∠PQR or ∠RQP . Similarly, in Fig. 4.22 (ii), we may write ∠B as ∠ABC or ∠CBA.

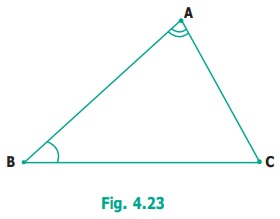
In the Fig. 4.23, two angles are marked.

Note that ∠BAC is not the same as ∠ABC, as they have different vertices and different sides

2. Measuring Angles

Can we measure angles too? Yes, they are measured in degrees and denoted by the symbol ‘ º ’. This has to be marked at top right of a number. We write angles as 35°, 78°, 90°, 110°, 145° and so on.

See that angles can be equal even if they are positioned differently.

3. Special Angles

Some angles are special. 90° is one such. We call it as the right angle.

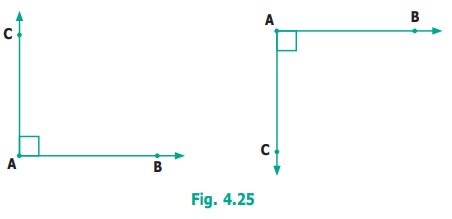
Right angle is most common in life. Examples can be seen at cross-roads, chess board, TV, etc.

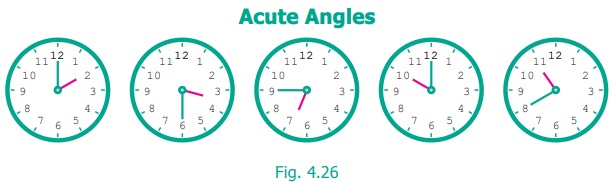
Acute Angles

Each of the angles in the above Fig. 4.26 is less than a right angle. Angles smaller than 90º are called Acute angles.

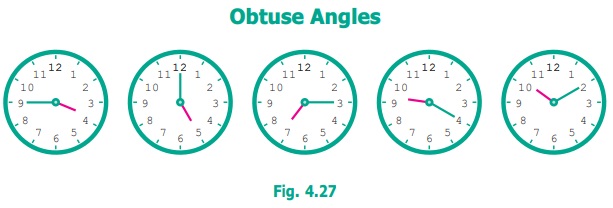
Obtuse Angles

Each of the angles in the above Fig. 4.27 is greater than right angle. Angles more than 90º are called Obtuse angles.

Activity

Stand facing the north side. Take a ‘right angle turn’ clockwise; you now face east. Again take another ‘right angle turn’ in the same direction. You now face south. Once again take another ‘right angle turn’ in the same direction. You now face west. Then follow the same you will come to the original position. Thus the complete turn is called one revolution. The turn from north to south will be two right angles. It is also called a straight angle. Two straight angles make one complete revolution. This is illustrated in the following figures.

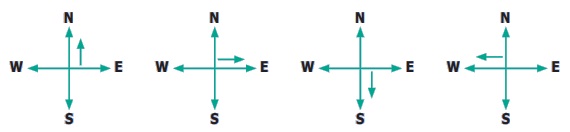
Try these

1. Which direction will you face if you start facing West and take three right turns clockwise?

Answer: South Direction

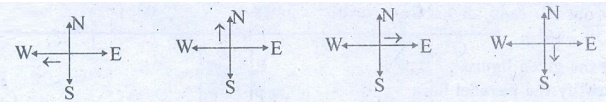
2. Which direction will you face if you start facing North and take two right turns anti-clockwise? 

Answer: South Direction