Questions with Answers, Solution | Measurements | Term 2 Chapter 2 | 7th Maths - Exercise 2.4 | 7th Maths : Term 2 Unit 2 : Measurements
Chapter: 7th Maths : Term 2 Unit 2 : Measurements
Exercise 2.4
Exercise
2.4
Miscellaneous
Practice problems
1. A wheel of a car covers a distance
of 3520 cm in 20 rotations. Find the radius of the wheel?
In 20 rotations the wheel of a car covers the distance = 3520 cm
In one rotation the wheel covers the distance = 3520 / 20 = 176
cm
Circumference ofthe circle 2πr = 176
2 × 22/7 ⊂ r = 176
r = 176×7 / 2×22 = 28 cm
The radius of the wheel = 28 cm
2. The cost of fencing a circular race
course at the rate of ₹8 per metre is ₹2112. Find the diameter of the race course.
The distance cover on fencing for ₹ 8 = 1 metre
The distance cover on fencing for ₹ 2112 = 2112 / 8 m
= 264 m
The circumference of the race course 2πr = 264 m
2
× 22/7 ⊂ r = 264
r = 264×7 / 2×22 = 42 m
Diameter d = 2r = 2 × 4 = 84 m
The diameter of the race course = 84 m
3. A path 2 m long and 1 m
broad is constructed around a rectangular ground of dimensions 120 m and
90 m respectively. Find the area of the path.

Inner area of the rectangular ground = 120 × 90 = 10800 m2
Outer area = (120 + 2×2) (90 + 2×1) m2
= (120 + 4) (90 + 2) m2
= 124 × 92 m2 =
11408 m2
The area of the path = Outer area – Inner area
= (11408 – 10800) m2
The area of the Path = 608 m2
4. The cost of decorating the circumference
of a circular lawn of a house at the rate of ₹55 per metre is ₹16940. What is the
radius of the lawn?
The distance decorated for ₹ 55 = 1 metre
The distance decorated for ₹ 16940 =16940 / 55 = 308 m
Circumference of the circle 2πr = 308 m
2 × 22/7 ⊂r = 308 m
r = 308×7 / 2×22 = 49 m
The radius of the lawn r = 49 m.
5.
Four circles are drawn side by side in a line and enclosed by a rectangle as shown
below. If the radius of each of the circles is 3 cm, then calculate:

(i)
The area of the rectangle.
(ii)
The area of each circle.
(iii) The shaded area inside the rectangle.
The radius of the circle = 3 cm
Length of the rectangle = 8 × radius
= 8 × 3 = 24 cm
Breath = 2 × radius
= 2 × 3 = 6 cm
i) The area of the rectangle = l × b
= 24 × 6 = 144 cm2
ii) Radius of a circle r = 3 cm
Area = πr2
The area of each circle = 22/7 × 3 × 3 = 198/7 = 28.28 cm2
iii) Area of a circle = 28.28 cm2
Area of 4 circles = 4 × 28.28 cm2
= 113.12 cm2
The shaded area inside the rectangle = Area ofthe rectangle – Area
of 4 circles.
= (144 – 113.12) cm2
= 30.88 cm2
Challenge
Problems
6.
A circular path has to be constructed around a circular lawn. If the outer and inner
circumferences of the path are 88 cm and 44 cm respectively, find
the width and area of the path.
Outer circumference of the circle = 88 cm
2 πR = 88 cm
R = [ 88 × 7 ] / [ 2 × 22 ] = 14 cm
Inner circumference = 44 cm
2 πr = 88 cm
R = 44×7 / 2×22 = 7 cm
The width of the path = R – r
= 14 – 7 = 7 cm
The area of the path = π (R2 – r2)
= 22/7 (142 –
72)
= 22/7 (196 – 49)
= 22/7 × 147 cm2
= 462 cm2
The area of the path = 462 cm2
7. A cow is tethered with a rope of length
35 m at the centre of the rectangular field of length 76 m and breadth
60 m. Find the area of the land that the cow cannot graze?
The area of the rectangle = 76 × 60 m2
= 4560 m2
The area of the land that cow can graze = Area of the circle of
radius
r = 35 m
Area of the land that cow can graze = πr2
= 22/7 × 35 × 35 m2
= 3850 m2
The area of the land that cow can not graze = Area of the
rectangle – Area of the land that cow can graze.
= (4560 – 3850) m2
The area of the land that cow can not graze = 710 m2.
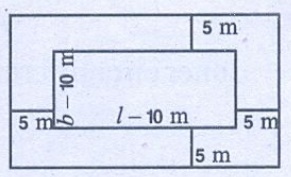
8. A path 5 m wide runs along
the inside of the rectangular field. The length of the rectangular field is three
times the breadth of the field. If the area of the path is 500 m2
then find the length and breadth of the field.
Length of outer rectangle =
l m
Outer breadth = b m
Width of the path = 5 m
Length of inner rectangle = l
– 2w = l – 10 m
Inner breadth = b – 2w
= b – 10m
Area of the outer rectangle = l x b m2
Area ofthe inner rectangle = (l – 10) (b – 10) m2
= (l b – 10 l –10 b + 100)m2
Area of the path = Area of the outer rectangle – Area of the
inner rectangle
= (l b –
lb + 10l + 10b – 100 = 500
= 10 (l + b) = 500 +
100 = 600 m2
= l + b = 600 / 10 =
60
Length of the rectangle = 3 times its breadth.
l = 3b
l + b = 60
3b + b = 60
4b = 60
b = 60 / 4 = 15 m
l = 3b = 3 × 15 = 45m
The length of the field = 45 m
Breadth = l5m
9. A circular path has to be constructed
around a circular ground. If the areas of the outer and inner circles are 1386 m2
and 616 m2 respectively, find the width and area of the path.
Area of the outer circle = 1386 m2
πR2 = 1386
R2 = 1386/22 ×
7 = 9 × 7 × 7
R = 3 × 7 = 21m
Area of the inner circle πr2 = 616
r2 = 616/22 × 7 = 4 × 7 × 7
r = 2 × 7 = 14 m
Width of the circle w = R – r
= 21 – 14 = 7 m
Area of the Path = Area ofthe outer circle – Area of the inner
circle.
= (1386– 616) m2
Area of the Pathe = 770 m2.
10. A goat is tethered with a rope of
length 45 m at the centre of the circular grass land whose radius is 52 m.
Find the area of the grass land that the goat cannot graze.
Radius ofthe circular grass land r = 52 m
Area of the grass land = ( 22/7) × 52 × 52 m2
Area of the grass land = 59488 / 7 = 8498.3 m2
The length ofthe tethered rope = radius r = 45 m
Area of the grass land that the goat can graze πr2 =
22/7 × 45 × 45m2
= 44550 / 7 = 6364.3 m2
Area of th grass land that the goat can not graze = Area of the
circle – Area of the grass land that the goat can graze.
= (8498.3 – 6364.3)m2
= 2134 m2
The area ofthe grass land that the goat cannot graze. = 2134m2
11. A strip of 4 cm wide is cut
and removed from all the sides of the rectangular cardboard with dimensions 30 cm
× 20
cm . Find the area of the removed portion and area of the remaining cardboard.
Area of the rectangular cardboard = 30 × 20 cm2
= 600 cm2
Width of the cutting portion w = 4 cm
Area ofthe inner rectanglre = (30 – 8) (20 – 8) cm2
= 22 × 12
cm2
Area of the cutting portion = 264 cm2
Area of the removed portion = Area of the rectangle – Area of
the cutting portion.
= (600 – 264) cm2
= 336 cm2
Area of the cutting portion = 264 cm2
Area of the removed portion = 336 cm2
12.
A rectangular field is of dimension 20 m × 15 m . Two paths run parallel
to the sides of the rectangle through the centre of the field. The width of the
longer path is 2 m and that of the shorter path is 1 m. Find (i) the
area of the paths (ii) the area of the remaining portion of the field (iii) the
cost of constructing the roads at the rate of ₹10 per sq.m.
Area of the longer path = 20 × 2 = 40 m2
Area of the shorter path = 15 × 1 = 15 m2
Area of the centre rectangle = 2 × 1 = 2 m2
Area of the path = (40 + 15 – 2) m2
= 53 m2
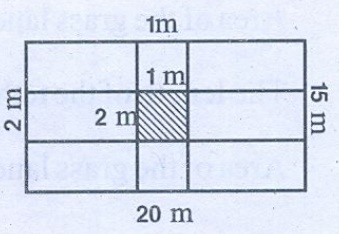
i) Area of the pathe = 53 m2
Area of the field = 20 × 15= 300m2
ii) Area of the remaining portion = Area of the field – Area of
the path.
= (300 – 53) m2 = 247 m2
iii) The cost of constructing the road of 1 sq.m = ₹ 10
The cost of constructing the road for 53 sq.m = ₹ 53 × 10
= ₹ 530
The cost of constructing the road = ₹ 530.
ANSWERS:
Exercise 2.4
1. 28 cm
2. 84 m
3.668 m2
4. 49 m
5. (i) 196 cm2 (ii) 38.5 cm2 (iii) 42 cm2
Challenge problems
6. 7 cm; 462 cm2
7. 710 m2
8. 30 cm; 10 cm
9. 7 m; 770 m2
10. 2134 m2
11. 264 cm2 ; 336 cm2
12. (i) 53 m2 (ii) 247 m2 (iii) ₹530
Related Topics