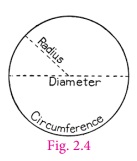
Circumference of a Circle

Circumference of a Circle

All circles are similar to one another. So, the ratio of the circumference to that of diameter is a constant, that is Circumference/ Diameter = constant [say π( pi ) ]

Its approate value is 3.14. Therefor C/d = π.

The diameter is twice the radius (2r), so the above equation can be written as C/2r = π.

Therefore, the circumference of circle, C = 2 πr units.

Obviously now, we see that Circumference, C = π d and d = 2r .

Thus for any circle with a given ‘r’ or ‘d’, we can find ‘C’ and vice-versa.

DO YOU KNOW

1. Calculation of decimal digits of π is an  interesting task asmong mathematans.

2. The constan π was used in the construction of popular pyraminds of Egypt.

3. Computer helped mathematicians to calculate the value of π with more than 12 trillion decimal digits.

Think

A circle has the shortest perimeter of all closed figures with the same area. Justify with an example.

Example 2.1

Calculate the circumference of the bangle shown in Fig. 2.5 (Take π = 3.14 ).

Solution

Given, d = 6 cm , d = 2r = 6 cm , r = 3cm

circumference of a circle = 2πr units

                                          = 2π × 3

                                         = 18.84

The circumference is 18.84 cm.

Example 2.2

What is the circumference of the circular disc of radius 14 cm? (use π = 22/7 ).

Solution

Radius of circular disc (r) = 14 cm

Circumference of the disc = 2 πr units

                                          = 2 × 22/7 ×14

                                           = 88 cm

Example 2.3

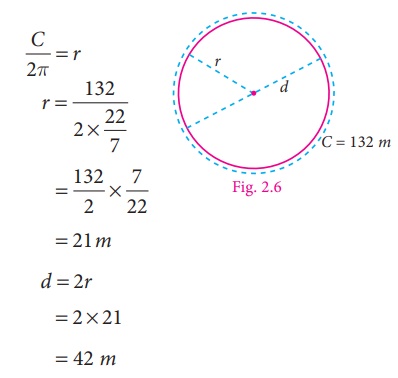
If the circumference of the circle is 132 m. Then calculate the radius and diameter (Take π=22/7 ).

Solution

Circumference of the circle, C = 2πr units

The circumference of the given circle = 132 m

Example 2.4

What is the distance travelled by the tip of the seconds hand of a clock in 1 minute, if the length of the hand is 56 mm (use π  = 22/7 ).

Solution

Here the distance travelled by the tip of the seconds hand of a clock in 1 minute is the circumference of the circle and the length of the seconds hand is the radius of the circle. So, r = 56 mm

Circumference of the circle, C = 2πr units

                                                = 2× (22/7) ×56

                                                = 2×22×8

                                                = 352 mm

Therefore, distance travelled by the tip of the seconds hand of a clock in 1 minute is 352 mm.

Example 2.5

The radius of a tractor wheel is 77 cm. Calculate the distance covered by it in 35 rotations? (use π = 22/7 ).

Solution

The distance covered in one rotation = the circumference of the circle

= 2 πr  units

= 2× (22/7) × 77

= 2×22×11

= 484 cm

The distance covered in one rotation = 484 cm

The distance covered in 35 rotations = 484 × 35

                                                          =16940 cm

Example 2.6

A farmer wants to fence his circular poultry farm with barbed wire whose radius is 420 m. The cost of fencing is ₹12 per metre. He has ₹30,000 with him. How much more amount will be needed to fence his farm? (Here π = 22/7)

Solution

The radius of the poultry farm is = 420 m

The length of the barbed wire for fencing the poultry farm is equal to the circumference

of the circle.

We know that the circumference of the circle = 2 πr units

                                                                         = 2 × (22/7) × 420

                                                                         = 2×22×60

The length of the barbed wire to fence the poultry farm = 2640 m

The cost of fencing the poultry farm at the rate of ₹12 per metre  = 2640 ×12

                                                                                                       = ₹31,680

Given that he has ₹30,000 with him.

The excess amount required = ₹31,680 − ₹30,000 = ₹1,680.

Example 2.7

Find the perimeter of the given shape (Fig.2.9) (Take π = 22/7 ).

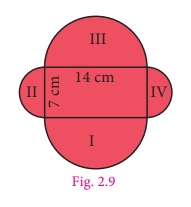
Solution

In this shape, we have to calculate the circumference of semicircle on each side of the rectangle. The outer boundary of this figure is made up of semicircles of two different sizes. Diameters of each of the semicircles are 7 cm and 14 cm. We know that the circumference of the circle = πd units.

Circumference of the semicircular part = ½ π d units

Hence, the circumference of the semicircle having diameter 7 cm is,

= (1/2) × (22/7) × 7 = 11 cm

Circumference of the pair of semicircular parts (II and IV) = 2 × 11 = 22 cm

Similarly, circumference of the semicircle having diameter 14 cm is,

 = (1/2) × (22/7) × 14 = 22 cm

Circumference of the pair of semicircular parts (I and III) = 2 × 22 = 44 cm .

Perimeter of the given shape = 22 + 44 = 66 cm .

Example 2.8

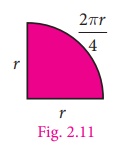
Kannan divides a circular disc of radius 14 cm into four equal parts. What is the perimeter of a quadrant shaped disc? (use π = 22/7)

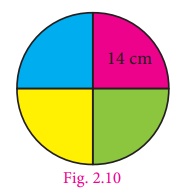
Solution

To find the perimeter of the quadrant disc, we need to find the circumference of quadrant shape.

Given that radius (r) = 14 cm.

We know that the circumference of circle = 2 πr units

.

So, the circumference of the quadrant arc = 1/4 × 2πr  

= πr / 2

= 22/7 × 14/2

= 22 cm

Given, the radius of the circle = 14 cm

Thus, perimeter of required quadrant shaped disc = 14 + 14 + 22

                                                                              = 50 cm .

Think

(i) Is the circumference of the semicircular arc and semicircular shaped disc same? Discuss.

(ii) The traffic lights are circular. Why?

(iii) When you throw a stone on still water in pond, ripples are circular. Why?