Measurements | Term 2 Chapter 2 | 7th Maths - Area of Pathways | 7th Maths : Term 2 Unit 2 : Measurements
Chapter: 7th Maths : Term 2 Unit 2 : Measurements
Area of Pathways
Area of Pathways
We come across pathways in different
shapes. Here we restrict ourselves to two kinds of pathways namely circular and
rectangular.
1. Circular Pathways
We observe around us circular shapes
where we need to find the area of the pathway. The area of pathway is the difference
between the area of outer circle and inner circle. Let ‘R’ be the radius
of the outer circle and ‘r’ be the radius of inner circle.

Therefore, the area of the circular pathway
= πR2 − πr2
= π(R2 − r2 ) sq. units.
2. Rectangular Pathways
Consider a rectangular park as shown
in Fig 2.23. A uniform path is to be laid outside the park. How do we find the area
of the path? The uniform path including the park is also a rectangle. If we consider
the path as outer rectangle, then the park will be the inner rectangle. Let l and b be the length and breadth of the park. Area of the park (inner rectangle)
= l b sq.units . Let w be the width of the path. If L, B are
the length and breadth of the outer rectangle, then L =
l + 2w and B = b +
2w .

Here, the area of the rectangular pathway
= Area of the outer rectangle – Area
of the inner rectangle
= (LB – lb) sq. units
Example 2.15
A park is circular in shape.
The central portion has playthings for kids surrounded by a circular walking pathway. Find the walking area whose
outer radius is 10 m and inner radius is 3 m.
Solution
The radius of the outer circle, R
=
10 m
The radius of the inner circle, r
=
3 m
The area of the circular path = Area
of outer circle − Area
of inner circle
= π R 2 −
πr2
= π( R2 −
r2 ) sq.units
= 22/7 × (102 − 32 )
= 22/7 × ((10 ×10) − (3 × 3))
= 227 × (100 − 9)
= 22/7 × 91
= 286 m2
Try these
(i) If the outer radius
and inner radius of the circles are respectively 9 cm and 6 cm, find
the width of the circular pathway.
Outer radius of the circle R = 9 cm
Inner radius r = 6 cm
The width of the pathway w = R – r
= 9 – 6 = 3 cm.
(ii) If the area of the
circular pathway is 352 sq.cm and the outer radius is 16 cm, find
the inner radius.
Area of the pathway = π (R2 – r2) = 352
sq.cm
Outer radius R = 16 cm
22/7 (162 – r2) = 352
256 – r2 = 352
/ 22 ⊂ 7 = 112
– r2 = 112 – 256 = – 144
r2 = 144 = 122
r = 12 cm
Inner radius = 12 cm
(iii) If the area of the inner rectangular region is 15 sq.cm
and the area covered by the outer rectangular region is 48 sq.cm, find the
area of the rectangular pathway.
Area of the outer rectangular region πR2 = 48 sq.cm
Area ofthe inner rectangular region πr2 =15 sq.cm
Area of the rectangular pathway = πR2 – πr2
= (48–15) sq.cm
= 33 sq.cm
Example 2.16
The radius of a circular
flower garden is 21 m. A circular path of 14 m wide is laid around the garden. Find the
area of the circular path.

Solution
The radius of the inner circle r
=
21 m
The path is around the inner circle.
Therefore, the radius of the outer circle,
R = 21 + 14 = 35 m
The area of the circular path =
π ( R 2 −
r2 ) sq.units
= 22 /7 × (352 −212)
= 22/7 × ((35 × 35) − (21 × 21))
= 22/7 × (1225
− 441)
= 22/7 ×
784
= 22 × 112 = 2464 m2
Example 2.17
The radius of a circular
cricket ground is 76 m. A drainage 2 m wide has to be constructed around the cricket ground for the purpose of draining
the rain water. Find the cost of constructing the drainage at the rate of ₹180/-
per sq.m.
Solution
The radius of the inner circle (cricket
ground), r = 76 m
A drainage is constructed around the
cricket ground.
Therefore, the radius of the outer circle,
R = 76 + 2 = 78 m
We have, area of the circular path = π( R 2 − r2 ) sq.
units
= 22/7 × (782
− 762 )
= 22/7 × (6084
− 5776)
= 22/7 × 308
= 22 × 44
= 968 m2
Given, the cost of constructing the drainage
per sq.m is ₹180.
Therefore, the cost of constructing the
drainage = 968 × 180 = ₹1,74,240.
Example 2.18
A floor is 10 m long and 8 m wide. A carpet of size 7 m long and 5 m wide is laid on the floor. Find the
area of the floor that is not covered by the carpet.
Solution
Here, L =
10 m
B = 8 m
Area of the
floor
= L × B
=10×8
=80 m2
Area of the
carpet
= l × b
= 7 × 5
= 35 m2
Therefore, the total area of the floor
not covered by the carpet = 80 – 35
=
45 m2
Example 2.19
A picture of length 23 cm and breadth 11 cm is painted on a chart, such
that there is a margin of 3 cm
along each of its sides. Find the total area of the margin.
Solution
Here L =
23 cm B = 11 cm
Area of the chart =
L × B
= 23 ×11
= 253 cm2
l = L −
2w =
23 −
2(3) =
23 −
6 =
17 cm
b = B −
2w =
11 −
2(3) =
11 −
6 =
5 cm2
Area of the picture 17× 5 = 85cm2
Therefore, the area of the marin =
235 − 85
= 168 cm2 .
Example 2.20
A verandah of width 3 m is constructed along the
outside of a room of length 9 m and width 7 m. Find (a) the area of the verandah
(b) the cost of cementing the floor of the verandah at the rate of ₹15 per sq.m.
Solution
Here, l =
9 m , b =
7 m
Area of the Room =
l × b
=9×7
= 63 m2
L = l +
2w =
8 +
2(3) =
8 +
6 =
14 m
B = b +
2w =
5 +
2(3) =
5 +
6 =
11 m
Area of the room including verandah =
L × B
= 14 ×11
= 154 m2
The area
of the verandah = Area of the room including verandah
− Area
of the room
=154−63
= 91 m2
The cost of cementing the floor for 1sq.m
= ₹15
Therfore, the cost of cementing the floor
of the verandah = 91 × 15 = ₹1365.
Example 2.21
A Kho-Kho ground has dimensions 30 m × 19 m which includes a lobby on all of its sides. The dimensions of the playing area is 27 m
× 16 m . Find the area of the lobby.
Solution
From the dimensions of the ground we
have,
L = 30 m ; B =
19 m ; l =
27 m ; b =
16 m
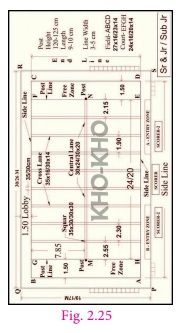
Area of the kho kho ground =
L × B
= 30 ×19
=
570 m2
Area of the play field =
l × b
= 27 ×16
=
432 m2
Area of the lobby =
Area of Kho-Kho ground − Area of the play field
= 570 – 432
=
148 m2
Related Topics