Measurements | Term 2 Chapter 2 | 7th Maths - Area of the Circle | 7th Maths : Term 2 Unit 2 : Measurements
Chapter: 7th Maths : Term 2 Unit 2 : Measurements
Area of the Circle
Area of the Circle
Let us consider the following situation.
A bull is tied with a rope to a pole.
The bull goes round to eat grass. What will be the portion of grass that the bull
can graze?
Can you tell what is needed to be found
in the above situation, Area or Perimeter? In this situation we need to find the
area of the circular region.
Let us find a way to calculate the area
(A) of a circle in terms of known
area, that is the area of a rectangle.
1. Draw a circle on a sheet of paper.
2. Fold it once along its diameter to
obtain two semicircles. Shade one half of the circle (Fig. 2.13)

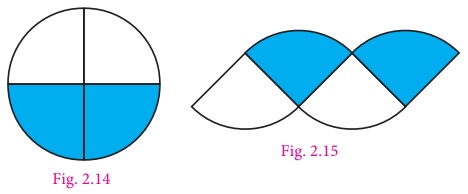
3. Again fold the semicircles to get
4 sectors. Fig. 2.14 shows a circle divided into four sectors. The sectors are re-arranged
and made into a shape as shown in Fig. 2.15.
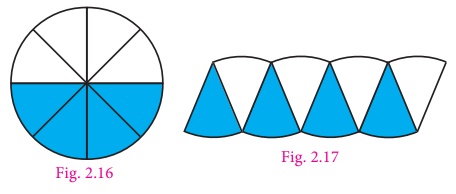
4. Repeat
this process of folding to eight folds, then it looks like a small sectors as shown
in the Fig. 2.16. The sectors are re-arranged and made into a shape as shown in
Fig. 2.17.
5. Press and unfold the circle. It is
then divided into 16 equal sectors and then into 32 equal sectors. As the number
of sectors increase the assembled shape begins to look more or less like a rectangle,
as shown in Fig. 2.19.
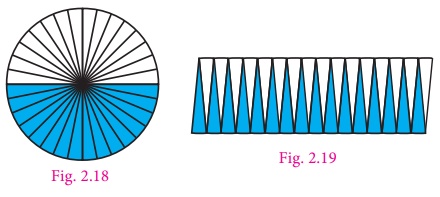
6. The top and bottom of the rectangle
is more or less equivalent to the circumference of the circle. Hence the top of
the rectangle is half of the circumference = πr . The height of the rectangle is
nearly equivalent to the radius of the circle. When the number of sectors is increased
infinitely, the circle can be rearranged to form a rectangle of length ‘ πr ’ and
breadth ‘r’.
We know that the area of the rectangle = l × b
= πr × r
=
π r2
= Area of the circle
So, the area of the circle, A
=
π r2 sq.units .
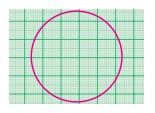
Activity
Draw circles of different
measurements on a graph sheet. Find the area by counting the number of squares enclosed
by the circle. So we get a rough estimate of the area of the circle.
Designs obtained by spirograph.
Shown below are some shapes
using a spirograph. We can observe that each of the different designs are circular.

Think
If the area and circumference
of the circle are equal then what will be the value of the radius?
Example 2.9
Find the area of the circle of radius
21 cm (Use π = 3.14 ).
Solution
Radius (r) = 21 cm
Area of a circle = πr2 sq.
units
= 3.14
× 21 × 21
= 1384.74
Area of the circle = 1384.74 cm2
Example 2.10
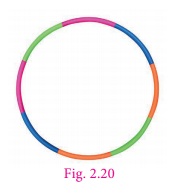
Find
the area of a hula loop whose diameter is 28 cm (use π
=
22/7).
Solution
Given the diameter (d) = 28 cm
Radius (r) = 28/2 = 14 cm
Area of a circle = πr2
sq.units
= 22/7 × 14 × 14
So, the area of the circle = 616 cm2.
Example 2.11
The area of the circular region is 2464
cm2. Find its radius and diameter. (use π
= 22/7)
Solution
Given that the area of the circular region
= 2464 cm2
πr2 = 2464
22/7 × r2 = 2464
r2 = 2464 × 7/22
r2 = 112 × 7 = 784
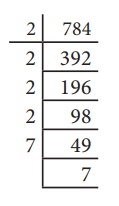
r2 =2×2×2×2×7×7
= 4×4×7×7
= 42 ×72
r2
= (4×7)2 [r×r
= (4×7)×(4×7)]
r = 4×7
= 28 cm
Diameter (d)
= 2 × r = 2 × 28 = 56 cm.
Example 2.12
A gardener walks around a circular park
of distance 154 m. If he wants to level the park at the rate of ₹25 per sq.m,
how much amount will he need? (use π =
22/7)
Solution
The distance covered by the man is nothing
but the circumference of the circle.
Given that the distance covered = 154 m
Therefore circumference of the circle
= 154 m
That is, 2πr = 154
2 × 22/7 × r
= 154
r
=154 × (7/44)
r
= 3.5 × 7
= 24.5
Area of the park = πr2 sq.units
= (22/7) × 24.5 × 24.5
= 22 × 3.5 × 24.5
= 1886.5 m2
Cost of levelling the park per sq.m = ₹ 25.
Cost of levelling the park of 1886.5
m2 = 1886.5 × 25 = ₹ 47,162.50
Example 2.13
Find the length of the rope
by which a cow must be tethered in order that it may be able to graze an area of 9856 sq.m (use π
=22/7)
Solution
Given that, the area of the circle = 9856 sq.m
πr2 = 9856
(22/7) ×
r2 = 9856
r2
= 9856 × 7/22
r2 = 448 × 7 = 3136

r2 = 2 × 2 × 2 × 2 × 2 × 2 × 7 × 7
r2
= 8 × 8 × 7 × 7 = 82 × 72 = (8 × 7)2
r
= 8 × 7 = 56 m
Therefore the length of the rope should
be 56 m.
Example 2.14
A garden is made up of a
rectangular portion and two semicircular
regions on either sides. If the length and width of the
rectangular portion are 16 m and 8 m respectively, calculate
(π = 3.14)
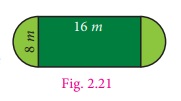
(i) the perimeter of the garden
(ii) the total area of the garden
Solution
(i) The perimeter of the rectangular
garden
Perimeter include two lengths each of
16 m and two semi circular arcs of diameter 8 m.
Circumference of the semicircle =
πd / 2 units
= [π × 8]
/2 = 4 π
= 4×3.14
=
12.56 m
Therefore, circumference of two semicircles
=
2 ×
12.56
=
25.12 m
Total perimeter = length + length + circumference
of two semicircles
= 16 +16 + 25.12
= 32 + 25.12
= 57.12 m
(ii) The total area of the garden
Total area of the garden = Area of rectangle
+ Area of 2 semicircles
= Area of
rectangle + Area of the circle
Here, the area of the rectangle = l × b
sq.units
=
16×8
= 128 m2
...(1)
Area of the circle = πr2
sq.units
= 3.14 ×4×4
= 3.14 × 16
= 50.24 m2 ...(2)
From (1) and (2), the total area of garden
= 128 + 50.24
= 178.24 m2
Try these
Draw circles of different radii on a graph paper. Find the area by
counting the number of squares covered by the circle. Also find the area by using
the formula.
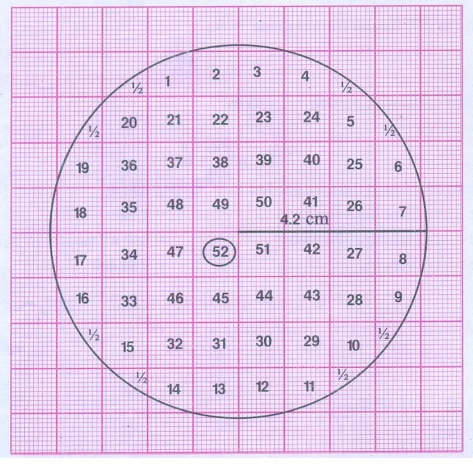
Number of squares covered by the circle = 52 + 8 × ½
= 52 + 4 = 56
Radius of circle r = 4.2 cm
Area of the circle = πr2
= 22/7 × 4.2 ⊂ 4.2 sq.cm
= 55.44 sq.cm
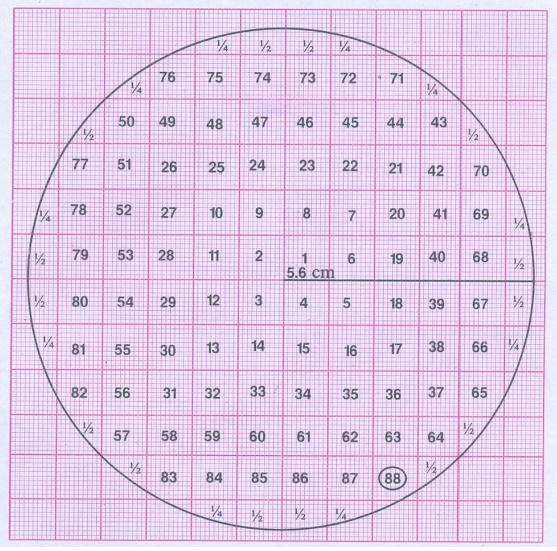
Number of squares covered by the circle = 88 +16 × ½ +10 × ¼
= 88 + 8 + 2 ½ = 98.5
Radius of the circle r = 5.6 cm
Area of the circle = πr2
= 22/7 × 5.6 ⊂ 4.2 sq.cm
= 98.56 sq.cm
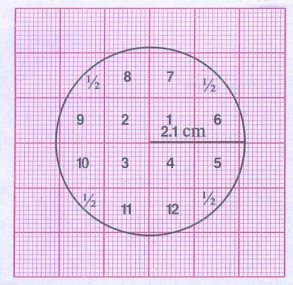
Number of squares covered by the circle =12 + 4 × ½
= 12 + 2 = 14
Radius r = 2.1cm
Area of the circle = πr2
= 22/7 × 2.1 ⊂ 21 sq.cm
= 13.86 sq.cm
(i) Find the area of the
circle, if the radius is 4.2 cm.
Radius of the circle r = 4.2 cm
Area of the circle = πr2
= 22/7 × 4.2 ⊂ 42 sq.cm
= 55.44 sq.cm
(ii) Find the area of the circle if the diameter is 28 cm.
Diameter of the circle d
= 28 cm
Radius r = 14 cm
Area of the circle = πr2
= 22/7 × 14 ⊂=14 sq.cm
= 616 sq.cm
Related Topics