Drug dose-effect relationships in biochemical cascades

Drug dose-effect relationships in biochemical cascades

We noted the similarity of empirical dose-effect relationships with theoretical plots (Figures 3.5a, 3.3, 3.4). This needs to be qualified in two ways:

1.  While the theoretical plots modeled receptor saturation, the experiment measured muscle tension.

2.  This similarity is by no means perfect.

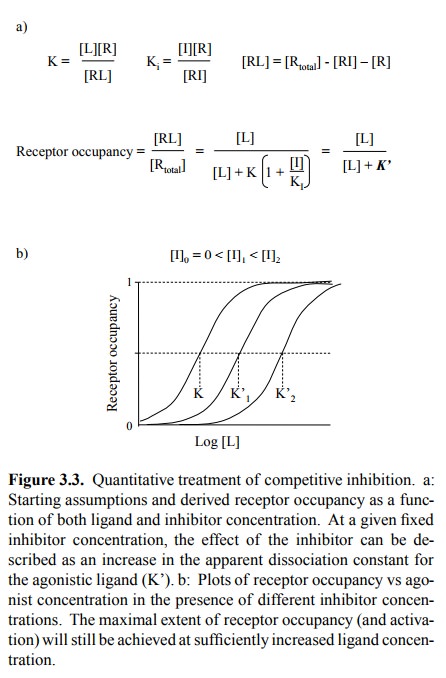
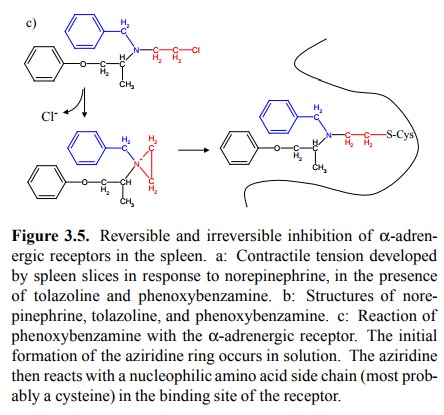
The two statements are in fact related. In our example, a perfect similarity of theoretical and experimental plots could only be expected if there were a linear relationship between receptor saturation with norepinephrine and mus-cle contraction. Considering that muscle contraction is trig-gered quite a bit downstream of receptor activation, there are numerous possible factors that will `distort' this lineari-ty, and in reality no linear relationship will ever be observed if drug target and drug effect are separated by intervening biochemical cascades. It thus turns out that the shape of a dose-effect relationship will depend very much on the func-tional proximity of the drug receptor molecule and the ob-served parameter.

If we can directly observe the function of the receptor, which thus at the same time is the effector, there will indeed be a linear relationship between the receptor interaction of a drug and its effect on function, respectively. As examples, we could name:

•     Enzymes – observed function: enzyme catalysis;

•     Ion channels – observed function: ion conductivity.

On the other hand, very often the observed effect is mea-sured a long way downstream of the drug receptor, as in our example of smoth muscle contraction and α-adrenergic blockers. Other such examples are

•     The inhibition of cyclooxygenase by acetylsalicylic acid, which results in a decrease in prostaglandin syn-thesis, with perceived pain relief as the functional read-out;

•     The activation or inhibition of nuclear hormone recep-tors by synthetic androgens, with a readout (way) down-stream of transcriptional regulation such as muscle growth or inhibition of sperm production (a highly edu-cational example, isn't it).

In cases like these, there will be numerous possible reasons for deviations from linearity in the dose-effect relationship. The deviations from linearity may of course take any shape; two typical effects are illustrated in Figure 3.6.

A hormone receptor typically triggers a biochemical cas-cade with multiple steps that need to occur before a func-tional effect is accomplished. This indirect coupling has surprising consequences for the relationship between the saturation of the receptor and that of the functional effect. We will consider the effect of cascading mediators in a very simple model⁶, containing the following assumptions (Fig-ure 3.7a):

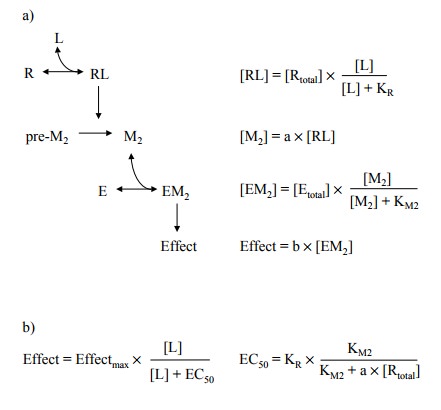
1.  The primary agonist (L) binds to the receptor (R) accord-ing to the law of mass action.

2.  The ligand-bound receptor promotes the formation of a second messenger (M₂), so that the concentration of M₂ is at all times proportional to the receptor occupancy, with a as their ratio. (This condition would be fulfilled if the rate of M₂'s formation were proportional to [RL], and M₂'s decay a first order process.)

3.  The second messenger (M₂) saturably binds to the effec-tor, and the observed effect is proportional to the extent of effector saturation with M₂.

From these fairly straightforward assumptions, the relation-ships summarized in Figure 3.7b and 3.7c can be derived.

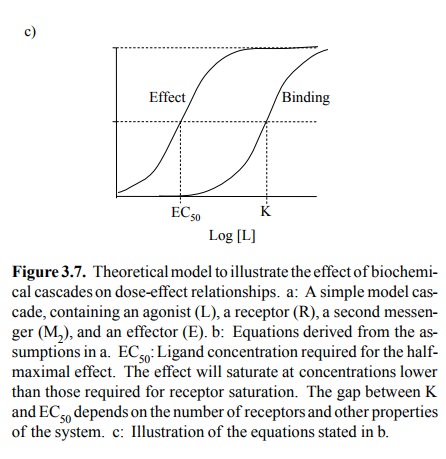
You can see that the relation between effect ligand concen-tration has the same shape as receptor occupancy. Howev er, the EC₅₀ – meaning the ligand concentration required for 50% of the maximum effect – is rather smaller than K _R, the equilibrium constant of receptor binding. Thus, sim-ply because receptor and effector are indirectly connected by means of a second messenger, the functional response of the system saturates at ligand concentrations that may be substantially lower than those required for saturating the receptor. Importantly, the gap between EC₅₀ and K_R will widen with increasing numbers of receptors. Thus, an in-crease in the number of receptors will always increase the sensitivity of the overall cascade to the ligand, even if all the components downstream of the receptor remain the same.

As an example of this effect, we may consider the stimula-tion of the heart by epinephrine, which acts on β-adrener-gic receptors. Half-maximal increase of heart muscle con-tractility (i.e., EC₅₀) is observed at 2% receptor saturation. Interestingly, β-receptors are subject to regulation by both covalent modification (phosphorylation) and reversible removal from the cell surface. Either process would re-duce the sensitivity of the system to epinephrine but leave the maximum response observed at receptor saturation unchanged.