Chapter: Physics : Dielectric Materials
Dielectric Materials
DIELECTRIC MATERIALS
1
Dielectrics
1.1
Properties
2
Fundamental definitions and Properties of electric dipole
3
Various polarization mechanisms involved in dielectric
3.1
Electronic polarization
3.2
Ionic polarization
3.3
Orientation polarization
3.4
Space charge polarization
3.5
Total polarization
4
Active and Passive Dielectrics
5
Frequency and Temperature on Polarization of Dielectrics
5.1
Frequency Dependence
5.2
Temperature Dependence
6
Internal field or Local field
6.1
Definition
6.2
Derivation
6.3
Clausius – Mosoti Equation
7
Dielectrics and Loss Tangent
7.1
Loss in purified gas
7.2
Loss in commercial dielectric
7.3
Power loss
8
Dielectric Breakdown
8.1
Types of dielectric breakdown
8.2
Remedies for breakdown mechanisms
9
General Applications
10
Applications of dielectric materials
10.1
Dielectrics in capacitors
10.2
Insulating materials in transformers
11
Ferro-electrics
11.1
Properties
11.2
Applications
1 DIELECTRICS
Solids which have an energy gap of three
eV or more are termed as insulators. In these materials, it is almost not
possible to excite the electrons from the valence band to conduction band by an
applied field. Generally dielectrics are also called as insulators, thereby
poor conductors of electricity. However they allow movement of some electrons
at abnormally high temperatures, causing a small flow of current.
Dielectrics are
non-metallic materials of high specific resistance ρ, negative temperature
coefficient of resistance (-α), largeandinsulation resistance. Insulation resistance will be affected by
moisture, temperature, applied electric field and age of dielectrics.
Dielectric materials are electrically non-conducting
materials such as glass, ebonite, mica,
rubber, wood and paper. All dielectric materials are insulating materials. The
difference between a dielectric and an insulator lies in their applications.
If the main function of non-conducting material is
to provide electrical insulation, then they are called as insulator. On the
other hand, if the main function of non-conducting material is to store
electrical charges then they are called as dielectrics.
1.1 PROPERTIES
Generally, the
dielectrics are non-metallic materials of high resistivity.
The have a
very large energy gap (more than 3eV).
All the
electrons in the dielectrics are tightly bound to their parent nucleus.
As there are
no free electrons to carry the current, the electrical conductivity of
dielectrics is very low.
They have
negative temperature coefficient of resistance and high insulation resistance.
2 FUNDAMENTAL
DEFINITIONS AND PROPERTIES ELECTRIC DIPOLE
A system consisting of two equal and
opposite charges n(+q, -q) separated by a distance (d) is called an electric
dipole.
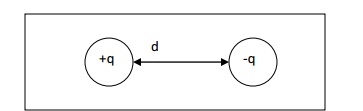
DIPOLE
MOMENT (Μ)
The product of the
magnitude of the charge (q) and distance between two charges (d) is called as
dipole moment.
Dipole
moment = qd (coulomb-metre)
PERMITTIVITY
(Ε)
The permittivity
represents the dielectric property of a medium. It indicates easily polarisable
nature of material. Its unit is farad/metre
DIELECTRIC
CONSTANT (Ε R)
A dielectric
characteristic of a material is determined by its dielectric constant. It is a
measure of polarisation of the dielectrics.
Definition
It is the
ratio between absolute permittivity of the medium (ε) and permittivity of free
space (εo).
Dielectric constant = Absolute permittivity (ε) / Permittivity of
free space (ε o)
εr=
εo / ε
POLARIZATION
Definition
The process of
producing electric dipoles inside the dielectric by the application of an
external electrical field is called polarization in dielectrics.
POLARISABILITY
(Α)
It is found that the
average dipole moment field (E).
It is found that the
average dipole moment field (E).
μ α
E
or μ
= α E
Where (α)
is the polarisability.
α = μ
/ E
Polarisability is
defined as the ratio of average dipole moment to the electrical field applied.
Its unit is farad m2.
Polarisation vector [Vactor P]
It is defined as the average dipole moment per unit
volume of a dielectric. If N is the number atoms per unit volume of a
dielectric and (μ)
is average dipole moment per atom, then

3 VARIOUS POLARIZATION MECHANISMS
INVOLVES IN DIELECTIC
Dielectric
polarization is the
displacement of charged
particles under the
action of the external electric field. There are number
of devices based on this concept. Those devices are rectifiers, resonators,
amplifiers and transducers, which converts electrical energy in to other forms
of energy.
Dielectric polarization
occurs due to several microscopic mechanisms.
Electronic polarization
Ionic polarization
Orientational
polarization
Space-charge
polarization
3.1 ELECTRONIC
POLARIZATION
Electronic polarization
occurs due to displacement of positively charged nucleus and negatively charged
electrons of an atom in the opposite directions on the application of an
electric field. This will result in the creation of dipole moment in the
dielectric.
Dipole moment (μ) is proportional
to the electric field strength (E).
μ α E
μ = α e E
Where (α e) is
proportionality constant and it is known as electronic polarizability.
Electronic polarization
takes place in almost all dielectrics.
Calculation of electronic polarizability
WITHOUT ELECTRIC FIELD
Consider an atom of a
dielectric material of nuclear charge Ze, where Z is the atomic number. The
electrons of charge (-Ze) are distributed uniformly throughout the atom
(sphere) of radius R as shown in fig.

The centres of the
electron cloud and the positive nucleus are at the same point and hence there
is no dipole moment.
Negative charge density
of an atom of radius R is given by
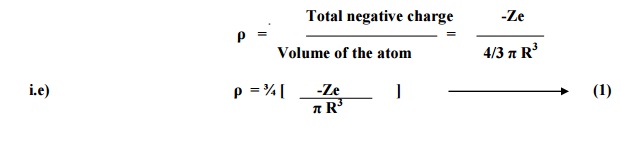
WITH ELECTRIC FIELD
When the atom of the dielectric is placed in an
electric field of strength E, two phenomenons occur.
Lorentz force (due to
electric field) will tend to move the nucleus and electron cloud of that atom
from their equilibrium positions. The positive nucleus will move towards the
field direction and the electron cloud will move in the opposite direction of
the field as shown in fig.
After separation, an
attractive coulomb force arises between the nucleus and the electron cloud
which will tend to maintain the original equilibrium position.
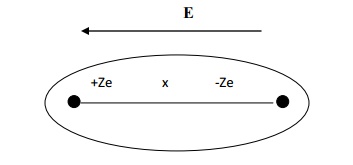
The electron cloud and
the nucleus move in opposite directions and they are separated by a distance x,
where there is a formation of electric dipole in the atom.
When these two forces
equal and opposite, there will be a new equilibrium between the nucleus and the
electron cloud of the atom.
Lorentz force between
the nucleus and the electron FL = charge x electrical field
= ZeE ---------(2)
Coulomb attractive
force between the nucleus and the electron cloud being separated at a distance
x,

Total number of negative charges
enclosed
In the sphere of radius x = charge
density x volume of the sphere of Radius x
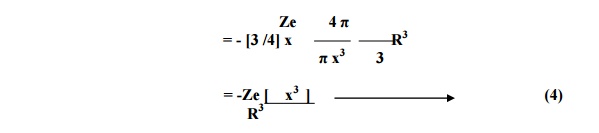
Total positive charge
of an atom present in the sphere of radius x,
Qp = + Ze
Substituting equation 4
in 3 we have
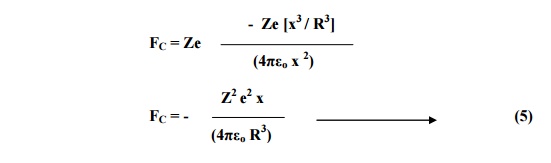
At equilibrium, Coulomb
force and Lorentz must be equal and opposite.
FL = - FC
Substituting for FL and
FC from equation 2 and 5 we have
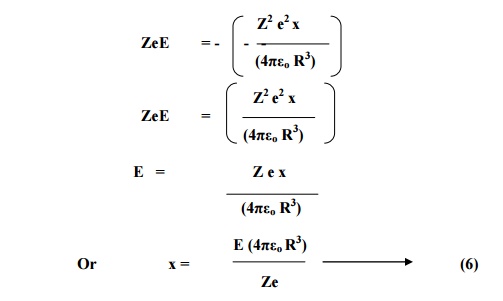
From the definition of
dipole moment, induced dipole moment (μ ind) is given by
μind = magnitude of charge x displacement
μind = Ze x
and dipole moment in terms of polarizability,
μind = αe
E -----(7)
Substituting the value
of x from 6 in 7 we have
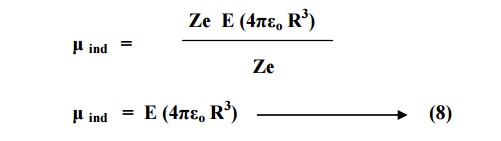
On comparing equation 8
and 9, we have
μind = α
e E
Where αe = 4πεo R3 is called electronic
polarizability.
Electronic polarization is independent of
temperature.
It is proportional to the volume of atoms in the
material.
Electronic polarization takes place in all
dielectrics.
3.2IONIC
POLARIZATION
Ionic polarization is due to the displacement of
catios (+ ve ions) and anions (- ve ions) in opposite directions. (e.g. NaCl
crystal) by the influence of external field.
When
an electric field (E) is applied on an ionic dielectric, there is shift of one
ion with
respect
to another from their mean position. The positive ion displace in the direction
of applied
electric
field through the distance x 1. The negative ions displace in opposite
direction trough the distance x2 as shown in the fig.

We
assume that there is one cation and one anion in each unit cell of that ionic
crystal.
Hence, the net distance between two ions
x = x1 + x2 -------(1)
When the ions are displaced from their mean position
in their respective directions the restoring forces appear which tend to ions
back to their mean position. The restoring force produced is proportional to
the displacement.
For positive ion
Restoring1 force
F α x
Or restoring force
acting on positive ion F = β1x1 ---------(2)
For negative ion
Restoring force
F α x2
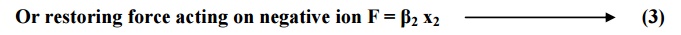
Where β1 and β2 are restoring force constants which depend up on the
masses of ions and angular frequency of the molecule in which ions are present.
If m is the mass of positive ion, M is the mass of negative ion and ωo is
the angular
frequency, then

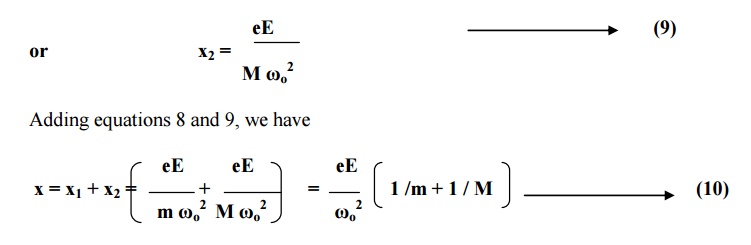
The dipole moment is equal to the product of charge and distance of separation between the charges.
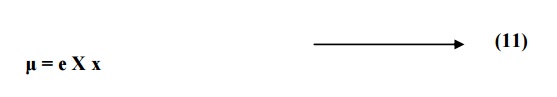
Substituting for x from
equation 10 in equation 11, we have

Conclusion
Ionic polarizability () is inversely proportional to the square of
angular frequency of the ionic molecule.
It is directly proportional to its reduced mass given by
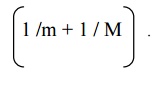
It is independent of temperature.
3.3 OREINTAIONAL
POLARIZATION
Orientational
polarization takes place only in polar dielectrics. Polar dielectrics have
molecules with permanent dipole moments even in the absence of external
electric field.
When the polar dielectrics are subjected
to external electric field, the molecular dipoles are oriented in the direction
of electric field.
The contribution to polarization due to
orientation of molecular diploes is called orientational polarization.
Orientational
polarization depends upon temperature when the temperature is increased ,
thermal energy tends to disturb the alignment.
From the Langevin’s
theory of paramagnetism , net intensity of magnetization
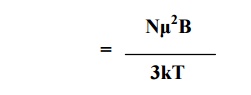
Since the same principle can be applied to the application of electric field in dielectrics, we may write
Orientational polarization,
Po =
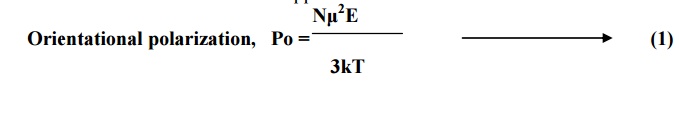
But, orientational
polarization is proportional to applied field (E) and it is given by
Po =o E Nα ----(2)
Comparing equations 1 and 2, we get

Conclusion
The orientation
polarizability is inversely proportional to absolute temperature of the
material.
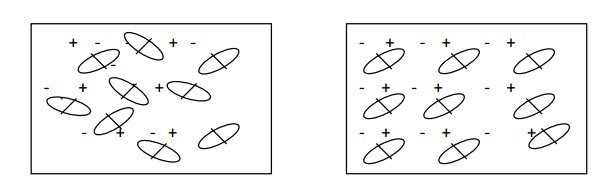
3.4 SPACE CHARGE
POLARIZATION
Space-charge polarization occurs due to accumulation
of charges at the electrodes or at the interfaces of multiphase dielectric
material.
When such materials subjected to an electrical field
at high temperature, the charges get accumulated as shown in fig. these charges
create diploes.
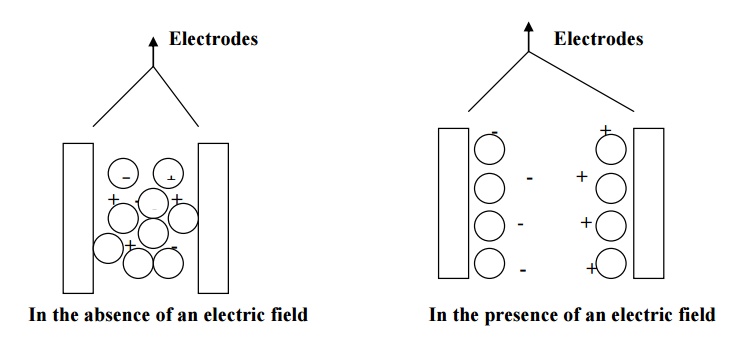
As a result, polarization is produced.
This kind of polarization is known as space-charge polarization. Space-charge
polarization is very small when compared to other polarization mechanisms and
it is not common in most of the dielectrics.
e.g- ferrites and semiconductors.
3.5 TOTAL POLARIZATION
α=e +αi+αo
Since the space- charge polarization is very small
and it is negligible.
Substituting the
corresponding expressions, we have
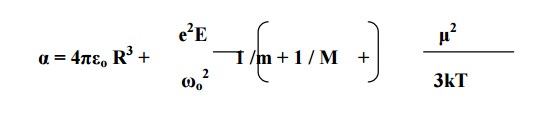
We know that the total polarization P = N E α
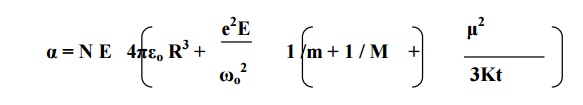
This equation is known
as Langevin –Debye equation
4 ACTIVE AND PASSIVE
DIELECTRICS
The dielectric materials may be classified as solid,
liquid and gas dielectrics.
In
solid form they may be polymeric such as nylon,
pvc, rubber, Bakelite, asbestos and wool or
may belong to the ceramic family such as glass,
silica, mica, porcelain, etc.
In
liquid form they may be mineral insulating oils,
synthetic insulating oils, tec.
In
gaseous form they may be air, nitrogen, sulphur
hexafluoride, inert gases etc.
The dielectrics can also be classified as active and passive dielectrics based on their applications.
Active Dielectrics
When dielectric is
subjected to external electric field, if the dielectric actively accept the
electricity, then they are termed as active dielectrics. Thus active
dielectrics are the dielectrics which can easily adapt itself to store the
electrical energy in it.
Examples:
Piezo-electrics, Ferro-electric etc.,
Passive Dielectrics
These dielectrics are
also called insulating materials. As the name itself suggest that it will act
as an insulator, conduction will not take place through this dielectrics. Thus passive
dielectrics are the dielectrics which restricts the flow of electrical
energy in it.
Examples:
All insulating materials such as glass, mica, etc.,
5 FREQUENCY AND
TEMPERATURE ON POLARISAION OF DIELECTRICS
When an alternating
electric field is applied across the material, polarization occurs as a
function of time.
Polarization as a function of time t is given by
P (t) = P [1 –e(-t/tr)]
Where P is
maximum polarization that occurs due to the static field applied for a long
time. tr is relaxation time.
5.1 FREQUENCY DEPENDENCE
Electronic polarization is the fastest polarization
which will complete at the instant the field is applied. The reason is that the
electrons are lighter elementary particles than ions.
Therefore even for very high frequency applied (in
the optical range) electronic polarization occurs during every cycle of the
applied field.
Ionic polarization is
little slower than electronic polarization. Because ions are heavier than the
electron cloud, the time taken for displacement is large. In addition the
frequency of applied field with which the ions will be displaced is equal to
the frequency of lattice vibration (10 13 Hz).
If the frequency of the
applied field is less than 10 13 Hz, the ions have enough time to
respond during each cycle of the applied field.
Orientational
polarization is even slower than ionic polarization. This type of polarization
occurs only at electrical frequency range (= 106Hz).
Space-charge
polarization is the slowest because have to diffuse over several atomic
distance. This process occurs at very low frequencies (102 Hz) as
shown in fig.
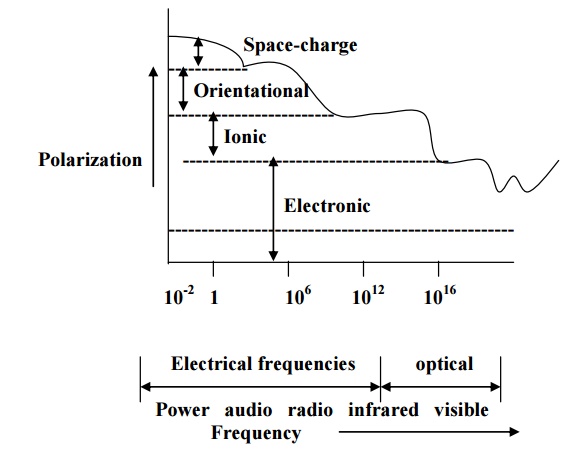
Figure explains the
four types of polarization at different frequency ranges. At optical
frequencies (-1015Hz), electronic polarization alone present. At -1013
Hz range, ionic polarization occurs in addition to electronic polarization.
At 106 to 1010
Hz range, contribution due to orientation polarization gets added while at 102
Hz range, space-charge polarization also contributes.
It is noted that at low
frequencies, all the four types of polarizations occur and total polarization
is very high.
Total polarization
decreases with increase in frequency and becomes minimum at optical frequency
range.
5.2TEMPERATURE
DEPENDENCE
When a dielectric material is subjected to ordinary conditions of
increasing temperature, electronic distribution in n the constituent molecules
are not affected.
Hence there will be no temperature influence on electronic and ionic
polarization mechanisms. Therefore electronic and ionic polarizations are
practically independent of temperature.
An increase in temperature brings a high degree of randomness in
molecular orientation of the material. This will affect the tendency of
permanent dipoles to align along direction of the field. Hence, orientation
polarization decreases with increase in temperature.
However in space-charge polarization, increase in temperature helps the
ion movement by diffusion. As a result it will increase the polarization.
Thus both the orientational and space-charge polarization mechanisms are
strongly temperature dependent.
6
INTERNAL FIELD OR LOCAL FIELD
6.1 DEFINITION
When a dielectric
material is placed in an external electric field, it produces an induced dipole moment.
Now, two fields are
acting at any point inside dielectrics are
Macroscopic electrical
field due to external electric field.
Electrical field due to
electric dipole moment.
These long range
coulomb fields produced due to dipoles is known as internal field or local
field. This internal field is responsible for polarization of each atom or
molecule in the solid.
6.2 DERIVATION
LORENTZ METHOD TO FIND
INTERNAL FIELD
The dielectric material
is uniformly polarized by placing it in between two plates of parallel plate
capacitor as shown in figure.
Assume an imaginary
spherical cavity around an atom for which the internal field must be calculated
at its centre.
The internal field (E int)
at the atom site is considered to be made up of the following four components.
E1, E2, E3 and E4.
E int = E1+
E2+ E3+E4
Where E1 –Electrical field due to charges
on the plates of the capacitor
E2 –Electric
field due to polarized charges (induced charges) on the plane surface of the
dielectric.
E3 –Electric
field due to polarized charges induced on the surface of the imaginary
spherical cavity.
E4 –Electric
field due to permanent dipoles of atoms inside the spherical cavity considered.
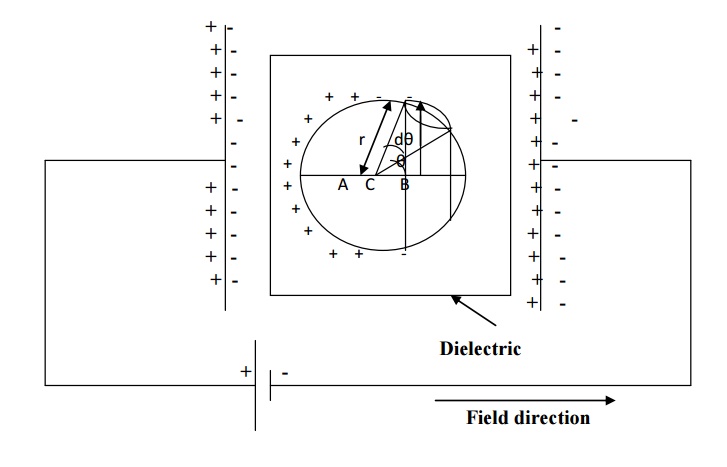
Macroscopically we can
take E = E1 + E2. i.e., the electrical field externally
applied (E1) and the electrical field induced on the plane surface
of the dielectric (E2) can be considered as a single electrical
field.
If we consider a
dielectric that is highly symmetric, the electrical field due to dipoles
present inside the imaginary cavity will cancel out of each other. Therefore
the electrical field due to permanent dipoles E4 = 0
Now, the equation (1) is rewritten as
E
int = E +E3
Calculation of E3
Let us consider small
area ds on the surface of the spherical cavity. It is confined within an angle
dθ at the angle θ in an direction of electric field
Polarization P is
parallel to E. PN is the component of polarization perpendicular to
the area ds as shown in the figure.
PN
= Pcosθ
q’ is
the area chargeds. Polarizationonisal so the defined as the surface charges
per unit area. q' / ds
PN = Pcosθ
= (q' /
ds)
Electric field
intensity at C due to charge q’ (Coulomb force) is given by
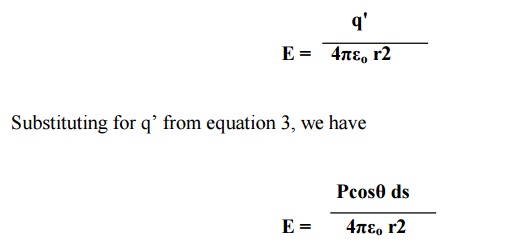
This electrical field
intensity is along the radius r and it can be resolved in to two components (Ex
and Ey) as shown in figure.
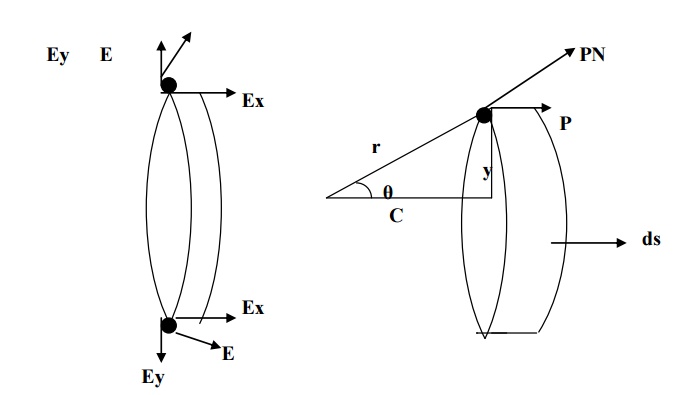
The component of intensity parallel to the
electrical field direction,
Ex = E
cosθ
Substituting for E from
equation 4 in 5, we have

The component of intensity perpendicular to the
field direction,
Ex
= E
sinθ
Since the perpendicular
components are in opposite directions, they cancel out each other. Hence, the
parallel components alone are taken onto consideration.
Now, consider a ring area dA which is
obtained by revolving ds about AB as shown in fig(b)

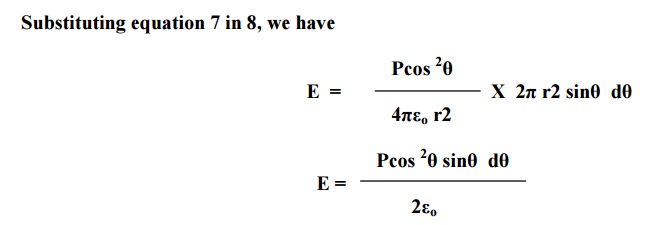
Electric field
intensity due to charges present in the whole sphere is obtained by integrating
equation 9 within the limits 0 to π. This electrical field is taken as E3.

Substituting equation
10 in equation 2, we get
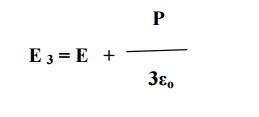
E int is the internal
field or Lorentz field.
6.3
CLAUSIUS – MOSOTI EQUATION
Let N be the number of
molecules per unit volume and α be the molecular polarizability.
Then
Total polarization, P =
N α Eint


Where εr is
dielectric constant.
Equation 5 is Clausius-
Mosotti relation which relates the dielectric constant (a macroscopic quantity) of the material with polarizability
(a microscopic quantity).
7 DIELECTRICS AND LOSS
TANGENT
If a dielectric is subjected to an electric field,
the electrical energy is absorbed by the dielectric and certain quantity of
electrical energy is dissipated in the form of heat energy. This is known as dielectric
loss.
The dielectric loss can occur both in direct and
alternating voltages. The dielectric loss is less in direct voltage than that
of the alternating voltage.
7.1LOSS
IN PURIFIED GAS
If an alternating
voltage is applied across the capacitor having vacuum or purified gas then the resulting current leads the applied
voltage by 90°, as shown in figure. If I lead V exactly by 90° we can say that
no electrical energy is lost.
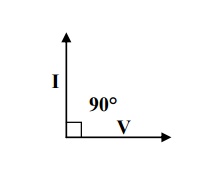
Explanation
We
know the power loss PL =
VI cosθ
When θ=90°;L P
7.2LOSS
IN COMMERCIAL DIELECTRIC
Now, when a practical
dielectric is present in the current leads the voltage by (90-δ), the shows that there is some loss in
electric energy and δ is called loss angle, as shown in fig.
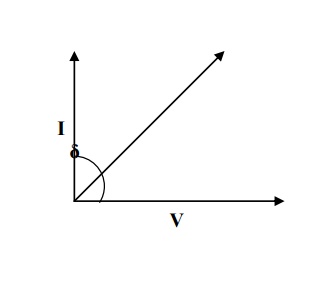
Explanation
In this case the power loss PL =
VIcosθ
Since- δθ=90; we L = VIcos have(90- δ)P
PL = VI sin
δ ------(1)
We know V = IR
I = V / R
If the capacitive resistance is Xc then we can write,
I = V / Xc (2)
Substituting equation 2 in 1, we get
7.3
POWER LOSS
Here
tan δ is called the power factor of the dielectric. If f, C, V are constants
then
PL
∞ tan δ
Naturally
the power loss varies with frequency. The power loss at various frequency
ranges is shown in fig.
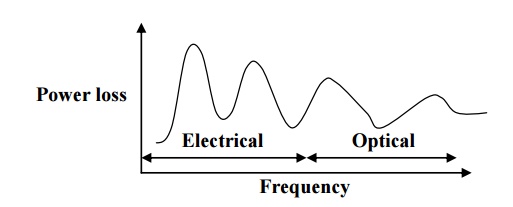
In
the electrical frequency regions the power is high, due to the diffusion of
ions from one equilibrium position to another.
In
the optical region the power loss is less because here the dielectric loss is
associated with electrons
8 DIELECTRIC BREAKDOWN
When a dielectric is
placed in an electric field and if the electric field is increased, when the
field exceeds the critical field, the dielectric loses its insulating property
and becomes conducting. i.e., large amount of current flows through it. This phenomenon
is called dielectric breakdown.
The
electric field strength at which the dielectric breakdown occurs is known as
dielectric
The dielectric strength = strength. Dielectric
voltage / Thickness of dielectric
8.1TYPES
OF DIELECTRIC BREAKDOWN
Intrinsic or avalanche breakdown
Thermal breakdown
Chemical and electrochemical breakdown
Discharge breakdown
Defect breakdown
INTRINSIC BREAKDOWN
When dielectric is subjected to electric field then
the electrons in the valance band acquire sufficient energy and go to
conduction band by crossing the energy gap and hence become conduction
electrons. Therefore large current flows and it is called intrinsic breakdown
or zener breakdown.
AVALANCHE BREAKDOWN
These conduction
electrons on further application of field then collide with the valance
electrons in the co-valent band and remove more electrons hence transferring
them as conduction electrons.
These secondary
conduction electrons again dislodge some other bound electrons in the valance
band and this process continues as a chain reaction. Therefore very large
current flows through the dielectrics and hence called as avalanche breakdown.
Characteristics
It can occur at lower temperatures.
It requires relatively large electric fields.
This kind of breakdown occurs in thin samples.
It occurs within short span of time
THERMAL BREAKDOWN
In general, when a
dielectric is subjected to an electric field, heat is generated. This generated
heat is dissipated by the dielectric. In some cases the heat generated will be
very high compared to the heat dissipated. Under this condition the temperature
inside the dielectric increases and heat may produce breakdown. This type of
breakdown known as thermal breakdown.
Characteristics
It occurs at higher temperatures.
It requires moderate electric
fields.
It depends on the size and shape
of the dielectric material.
It occurs in the order of
milliseconds.
CHEMICAL AND ELECTROCHEMICAL BREAKDOWN
This type of breakdown
is almost similar to the thermal breakdown. If the temperature is increased
mobility of ions will increase and hence the electrochemical reaction may be
induced to take place.
Therefore when mobility
of ions increased, insulation decreases and hence dielectrics becomes
conducting. This type of breakdown is called as chemical and electrochemical
breakdown.
Characteristics
It occurs only at low temperatures.
It depends on concentration of ions, magnitude of leakage current.
It occurs even in the absence of electric field.
DISCHARGE BREAKDOWN
Discharge breakdown
occurs when a dielectric contains occluded air bubbles as shown in fig. when
this type of dielectric subjected to electrical field, the gases present inside
the material will easily ionize and thus produce large ionization current. This
is known as discharge breakdown.
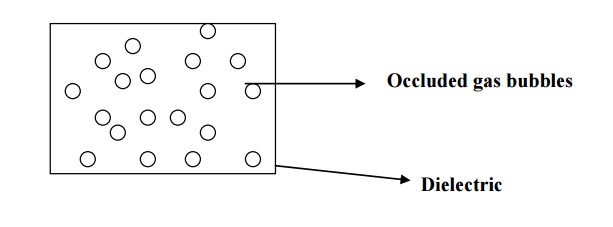
Characteristics
It occurs at low voltages.
It occurs due to the presence of occluded air bubbles.
It depends upon the frequency of the applied voltage.
DEFECT BREAKDOWN
Some dielectric have defects
such as cracks, pores, blow holes etc. these vacant position may have moisture
which leads to breakdown called as defect breakdown.
8.2 REMEDIES FOR
BREAKDOWN MECHANISMS
To avoid breakdown, the
dielectric material should have the following properties.
It should have high resistivity.
It must possess high dielectric strength.
It should have sufficient mechanical strength.
Dielectric loss should be low.
Thermal expansion should small.
It should be fire proof.
It should resistive to oils, liquids and gases.
It must have less density.
There should not be any defects.
It must be in pure form.
9 GENERAL APPLICATIONS
The following are the some of the applications of
the dielectric materials:
2. Quartz
crystal is used for the preparation of ultrasonic transducers, crystal
oscillators, delay lines, filters etc.
3. Barium
Titanate is used for the preparation of accelerometers.
4. Lead
Zirconate Titanate (PbZrx Ti1-x O3) is used
for the preparation of earphones, microphones, spark generators (gas lighter,
car ignition), displacement transducer, accelerometers etc.
5. Mica
is used in electrical machines, switch gears, armature winding, hot plates etc.
6. Dielectric
materials are used as an insulating material in power cables, signal cables,
electric motors, circuit breakers etc.
7. In
radiation detectors, thermionic valves and electric devices, the dielectric
materials are used.
8. The
pyroelectric materials are used as radiation detector.
9. The
dielectric materials are used in strain gauges, capacitors and resistors.
10.
The electro-optic devices are prepared
using dielectric material.
10 APPLICATIONS OF
DIELECTRIC MATERIALS
Almost all electrical
devices depend on insulating material in some way or other. Insulating
materials are used in power and distribution transformers, rotating machines,
capacitors, cables, and electronic applications.
10.1 DIELECTRICS IN CAPACITORS
For dielectrics used in
capacitors, it should possess the following properties.
It must have high dielectric constant.
It should possess high dielectric strength.
It should have high specific resistance.
It should also have low dielectric loss.
Uses
Thin sheets of papers filled with synthetic oils are used as dielectrics
in the capacitors.
Tissue papers and polypropylene films with dielectrol are used in power
capacitors.
Mica used as dielectrics in discrete capacitor.
An electrolytic solution of sodium phosphate is used in wet type
electrolytic capacitors.
Ceramic materials such as barium titanate and calcium titanate are used
in disc capacitors and high frequency capacitors respectively.
10.2 INSULATING MATERIALS IN
TRANSFORMERS
For dielectrics to act as insulating materials, it
should possess the following properties.
It should have low dielectric resistant.
It should possess low dielectric loss.
It must have high resistance.
It must possess high dielectric strength.
It must have high moisture resistance.
It should have adequate chemical stability.
Uses
Ceramics and polymers are used as insulators.
Paper, rubber, plastics, waxes etc are used to form thin films, sheets,
tapes, rods, etc. PVC, is used to manufacture pipes, batteries, cables etc.
Glass, mica, asbestos, alumina are used in ceramics.
Liquid dielectrics such as petroleum oils, silicone oils are widely used
in transformers, circuit breakers, etc.
Synthetic oils such as askarels, sovol, etc are used as coolent and
insulant in high voltage transformers.
11 FERRO-ELECTRICITY
AND APPLICATIONS
Ferro –electricity
When a dielectric
material exhibits electric polarization even in the absence of external field,
it is known as ferro-electricty and these materials termed as ferro-electric.
11.1 FERRO-ELECTRICS
Ferro-electrics are
anisotropic crystals which exhibit spontaneous polarization, i.e. they exhibit
polarization even in the absence of external electric field.
Examples
Rochelle salt,
Potassium niobate,
Lithium tentalate,
Ammonium dihydrogen phosphate,
Potassium dihydrogen phosphate,
Barium titanate.
11.2 PROPERTIES
The dielectric constant of these ferro-electric materials is above 2000
and it will not vary with respect temperature.
The dielectric constant(ε) reaches maximum value only at a particular
temperature called Curie temperature.
The polarization does not varies linearly with respect to electric field
and hence these materials are also called as non-linear dielectrics.
Ferro-electric exhibits electric polarization easily, even in the absence
of external electric field. They exhibit domain structure similar to that of a
Ferro-electric material.
Ferro-electric materials also exhibit hysteresis, similar to that of
ferromagnetic materials.
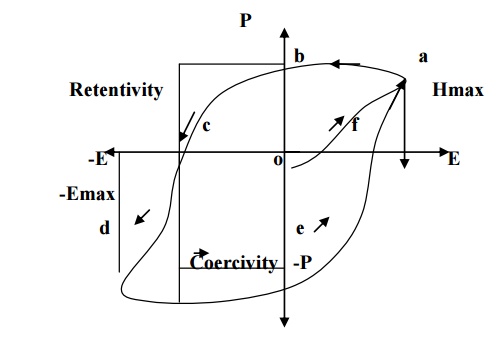
11.3 APPLICATIONS
Ferro-electric materials are used to produce ultasonics
They are used in production of piezo-electric materials and in turn to
make micro phones. Ferro-electrics are also used in SONAR, strain gauges, etc.
Ferro-electric semiconductors are used to make positors, which is turn
are used to measure and control the temperature.
They are also used as frequency stabilizers and crystal controlled
oscillators.
Electrets are a type of ferro-electric materials, used in the production
of capacitor microphones, gas filters, etc.
Electrets are also used to bond the fractured bones in the human body.
Pyro-electric materials are also used to produce high sensitive infrared
detectors.
Related Topics