Control System Analysis/ Closed Loop Analysis of PLL

Control System Analysis/ Closed Loop Analysis of PLL

Phase locked loops can also be analyzed as control systems by applying the Laplace transform.

The loop response can be written as:

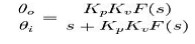
Where

·           θo is the output phase in radians

·           θi is the input phase in radians

·           Kp is the phase detector gain in volts per radian

·           Kv is the VCO gain in radians per volt-second

·           F(s) is the loop filter transfer function (dimensionless)

The loop characteristics can be controlled by inserting different types of loop filters. The simplest filter is a one-pole RC circuit. The loop transfer function in this case is:

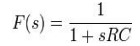
The loop response becomes:

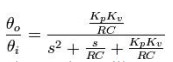
This is the form of a classic harmonic oscillator. The denominator can be related to that of a second order system:

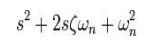
Where 

ζ is the damping factor

ωn is the natural frequency of the loop.

For the one-pole RC filter,

The loop natural frequency is a measure of the response time of the loop, and the damping factor is a measure of the overshoot and ringing. Ideally, the natural frequency should be high and the damping factor should be near 0.707 (critical damping). With a single pole filter, it is not possible to control the loop frequency and damping factor independently. For the case of critical damping,

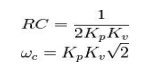
A slightly more effective filter, the lag-lead filter includes one pole and one zero. This can be realized with two resistors and one capacitor. The transfer function for this filter is

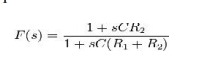
This filter has two time constants

τ1 = C(R₁ + R2) τ₂

=CR₂

Substituting above yields the following natural frequency and damping factor

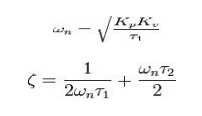
The loop filter components can be calculated independently for a given natural frequency and damping factor

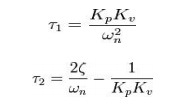
Real world loop filter design can be much more complex eg using higher order filters to reduce various types or source of phase noise.

Applications of PLL:

The PLL principle has been used in applications such as

·           FM stereo decoders

·           motor speed control

·           tracking filters

·           FM modulation and demodulation

·           FSK modulation

·           Frequency multiplier

·           Frequency synthesis etc.,

Example PLL ICs:560 series (560, 561, 562, 564, 565 & 567)