Analog Multiplier ICs

Analog Multiplier ICs

Analog multiplier is a circuit whose output voltage at any instant is proportional to the product of instantaneous value of two individual input voltages.

Important applications of these multipliers are multiplication, division, squaring and square – rooting of signals, modulation and demodulation.

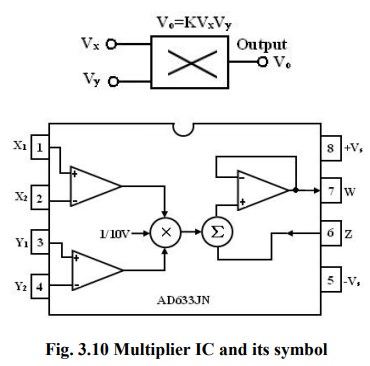
These analog multipliers are available as integrated circuits consisting of op-amps and other circuit elements. The Schematic of a typical analog multiplier, namely, AD633 is shown in figure.

·           The AD633 multiplier is a four – quadrant analog multiplier.

·           It possesses high input impedance; this characteristic makes the loading effect on the signal source negligible.

·           It can operate with supply voltages ranging from ±18V.

·           IC does not require external components.

·           The typical range of the two input signals is ±10V.

Schematic representation of a multiplier:

The schematic representation of an analog multiplier is shown in figure. The output V₀ is the product of the two inputs V_x and V_y is divided by a reference voltage V_ref. Normally, the reference voltage V_ref is internally set to 10V. Therefore, V0 =V_xV_y/10. In other words, the basic input – output relationship can be defined by KV_x V_y when K = 1/10, a constant. Thus for peak input voltages of 10V, the peak magnitude of output voltage is 1/10 *10 *10 =10V. Thus, it can be noted that, as long as V_x < 10V and V_y < 10V, the multiplier output will not saturate.

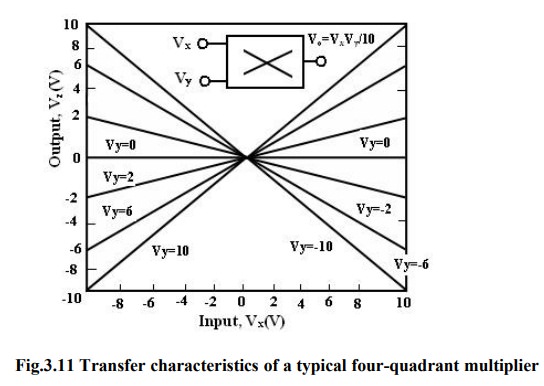
Multiplier quadrants:

The transfer characteristics of a typical four-quadrant multiplier are shown in figure. Both the inputs can be positive or negative to obtain the corresponding output as shown in the transfer characteristics.

Applications of Multiplier ICs:

The multiplier ICs are used for the following purposes:

1.        Voltage Squarer

2.        Frequency doublers

3.        Voltage divider

4.        Square rooter

5.        Phase angle detector

6.        Rectifier

Voltage Squarer:

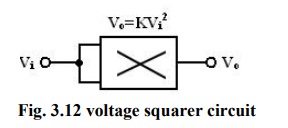
Figure shows the multiplier IC connected as a squaring circuit. The inputs can be positive or negative, represented by any corresponding voltage level between 0 and 10V. The input voltage V_i to be squared is simply connected to both the input terminals, and hence we have, V_x = V_y = V_i and the output is V0 = KVi2. The circuit thus performs the squaring operation. This application can be extended for frequency doubling applications.

Frequency doublers:

Figure shows the squaring circuit connected for frequency doubling operation. A sine-wave signal Vi has a peak amplitude of Av and frequency of f Hz. Then, the output voltage of the doublers  circuit is given by

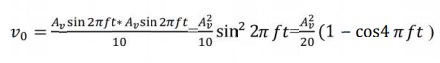
Assuming a peak amplitude Av of 5V and frequency f of 10KHz, V0 =1.25–1.25 cos2 20000) t. The first term represents the dc term of 1.25V peak amplitude. The input and output waveforms are shown in figure. The output waveforms ripple with twice the input frequency in the rectified output of the input signal. This forms the principle of application of analog multiplier as rectifier of ac signals.

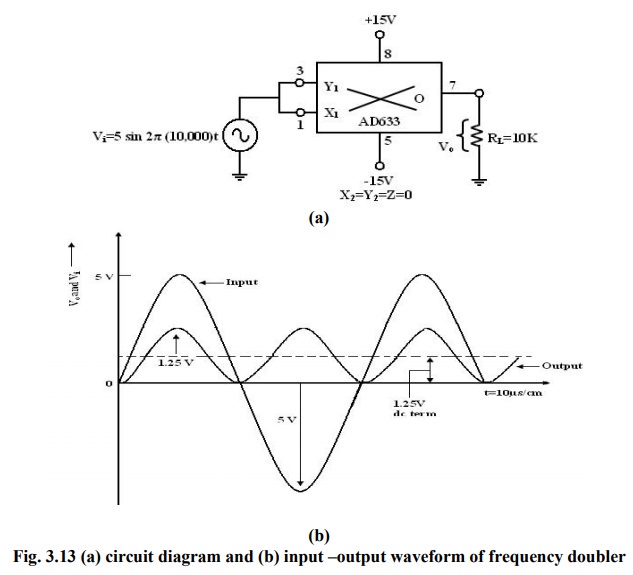
The dc component of output V₀ can be removed by connecting a 1µF coupling capacitor between the output terminal and a load resistor, across which the output can be observed.

Voltage Divider:

In voltage divider circuit the division is achieved by connecting the multiplier in the feedback loop of an op-amp.

The voltages V_den and V_num represent the two input voltages, Vdm forms one input of the multiplier, and output of op-amp VoA forms the second input.

The output V_OA forms the second input. The output VOM of the multiplier is connected back of op- amp in the feedback loop. Then the characteristic operation of the multiplier gives

V_om = KV_OA Vdm (1)

As shown in figure, no input signal current can flow into the inverting input terminal of op-amp, which is at virtual ground. Therefore, at the junction a, i₁ + i₂ =0, the current i1 = V_num / R, where R is the input resistance and the current i₂ = V_om /R. With virtual ground existing at a,

i₁+i₂ = V_num / R + V_om /R = 0

KV_OA V_den = - V_num

 or

voA=- v_num/Kv_den

where V_num and V_den are the numerator and denominator voltages respectively. Therefore, the voltage division operation is achieved. V_num can be a positive or negative voltage and V_den can have only positive values to ensure negative feedback. When Vdm is changed, the gain 10/V_dm changes, and this feature is used in automatic gain control (AGC) circuits.

Square Rooter:

The divider voltage can be used to find the square root of a signal by connecting both inputs of the multiplier to the output of the op-amp. Substituting equal in magnitude but opposite in polarity (with respect to ground) to Vi. But we know that Vom is one- term (Scale factor) of V0 * V0 or -V_i = V_om = V²/1 0

Solving for V₀ and eliminating √-1 yields. V0 = √10|Vi |

Eqn. states that V₀  equals the square root of 10 times the absolute magnitude of V_i.

The input voltage Vi must be negative, or else, the op-amp saturates.

The range of Vi is between -1 and -10V. Voltages less than -1V will cause inaccuracies in the result.

The diode prevents negative saturation for positive polarity Vi signals. For positive values of Vi the diode connections are reversed.

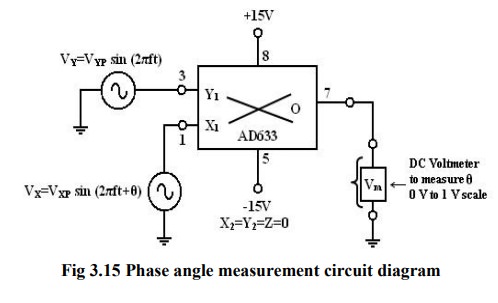
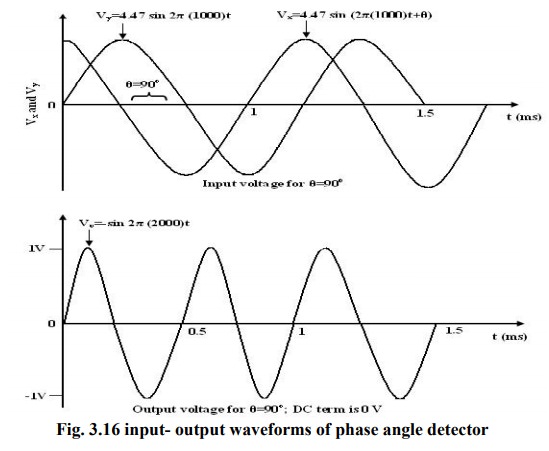
Phase Angle detector:

The multiplier configured for phase angle detection measurement is shown in figure. When two sine-waves of the same frequency are applied to the inputs of the multiplier, the output V0 has a dc component and an AC component.

The trigonometric identity shows that Sin A sin B =1/2 (cos (A-B) – cos (A+B)).

When the two frequencies are equal, but with different phase angles, e.g. A=2πft +θ for signal Vx and B= 2πft for signal V_y, then using the identity

[sin (2 ft+ )][sin2 ft)]=1/2[cos -cos(4 ft + )]=1/2(dc- the double frequency term)

Therefore, when the two input signals V_x and V_y are applied to the multiplier, V₀ (dc) is given by

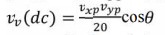
where V_xp and V_yp are the peak voltage amplitudes of the signals V_x and V_y. Thus, the output V₀(dc) depends on the factor cos θ. A dc voltmeter can be calibrated as a phase angle meter when the product of V_xp and V_yp is made equal to 20. Then, a (0-1) V range dc voltmeter can directly read cos θ, with the meter calibrated directly in degrees from a cosine table. The input and output waveforms are shown in figure.

Then the above eqn becomes V₀ (dc) = cos θ, if we make the product V_xp V_yp = 20 or in other words, V_xp – V_yp = 4.47V.