Chapter: Digital Electronics : Combinational Circuits
Comparator
COMPARATOR :
Comparator compares binary numbers.
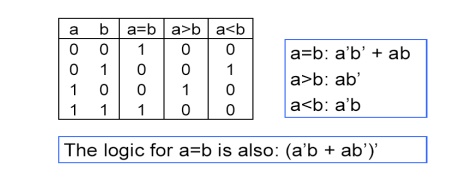
Logic comparing 2 bits: a and b
Magnitude Comparator
Comparator compares binary numbers 4-bit Magnitude Comparator:
Inputs: A3A2A1A0 & B3B2B1B0
Outputs: Y A>B, Y A<B, Y A=B For each bit, let:
Si = AiBi + Ai’Bi’ = (AiBi’ + Ai’Bi)’
Si is true when Ai = Bi
For A = B, we must have:
A3=B3 and A2=B2 and A1=B1 and A0=B0
Hence, Y A=B = S3•S2•S1•S0 136
Logic For A > B
For A > B, there are 4 cases:
1. A3B3 is 10 and A2A1A0 & B2B1B0 can be anything:
A=1xxx, B=0xxx
2. A3=B3 and A2B2 is 10 and A1A0 & B1B0 can be anything: A=11xx, B=10xx or A=01xx, B=00xx
3. A3=B3 and A2=B2 and A1B1=10 and A0B0 is xx: e.g.
A=011x, B=010x
4. A3=B3 and A2=B2 and A1=B1 and A0B0 is 10: e.g. A=1011, B=1010
Y A>B=A3B3’+S3A2B2’+S3S2A1B1’+S3S2S1A0B0’
Logic For A < B
For A < B, there are also 4 cases:
1) A3B3 is 01 and A2A1A0 & B2B1B0 can be anything:
A=0xxx, B=1xxx
2) A3=B3 and A2B2 is 01 and A1A0 & B1B0 can be
anything: A=10xx, B=11xx or A=00xx, B=01xx
3) A3=B3 and A2=B2 and A1B1=01 and A0B0 is xx: e.g.
A=110x, B=111x
4) A3=B3 and A2=B2 and A1=B1 and A0B0 is 01: e.g.
A=1000, B=1001
Y A<B=A3 ’B3+S3A2 ’B2+S3S2A1 ’ B1+S3S2S1A0 ’ B0
4-bit Comparator Logic Circuit
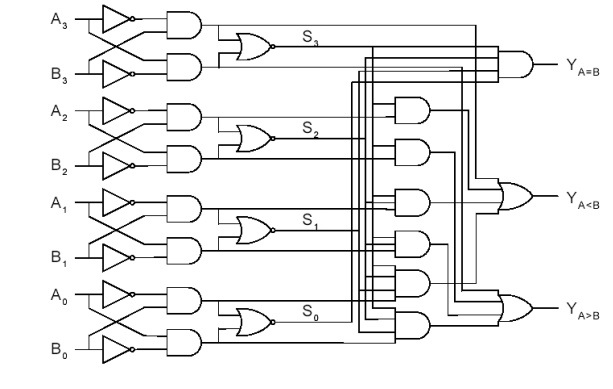
MSI: 7485 4-bit Magnitude Comparator
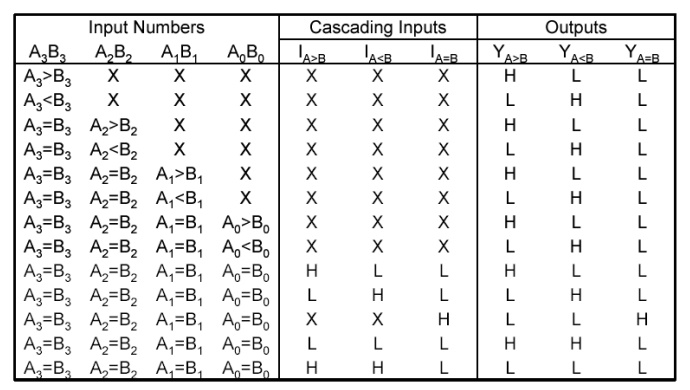
Comparison of 4-bit Numbers

Comparison of 8 - bit Numbers
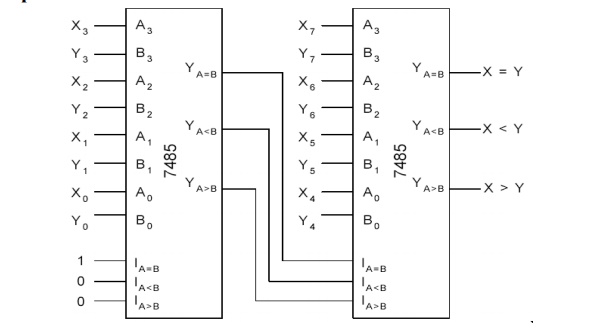
Related Topics