Chapter: Digital Logic Circuits : VHDL
Combinational logic
Combinational logic
In digital circuit theory, combinational logic
(sometimes also referred to as combinatorial logic) is a type of digital logic
which is implemented by boolean circuits, where the output is a pure function
of the present input only. This is in contrast to sequential logic, in which
the output depends not only on the present input but also on the history of the
input. In other words, sequential logic has memory while combinational logic
does not.
Combinational logic is used in computer circuits
to do this Boolean algebra on input signals and on stored data. Practical
computer circuits normally contain a mixture of combinational and sequential
logic. For example, the part of an arithmetic logic unit, or ALU, that does
mathematical calculations is constructed using combinational logic. Other
circuits used in computers, such as half adders, full adders, half subtractors,
full subtractors, multiplexers, demultiplexers, encoders and decoders are also
made by using combinational logic.
Representation
Combinational logic is used for building
circuits where certain outputs are desired, given certain inputs. The
construction of combinational logic is generally done using one of two methods:
a sum of products, or a product of sums. A sum of products can be easily
visualized by looking at a truth table:
A B C Result Logical equivalent

Using sum of products, we take the sum of all
logical statements which yield true results. Thus, our result would be:
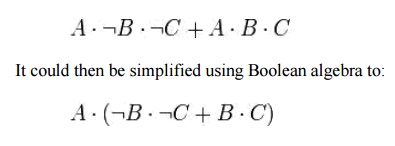
Logic formulas minimization
Minimization (simplification) of combinational
logic formulas is produced on the basis of the following rules:
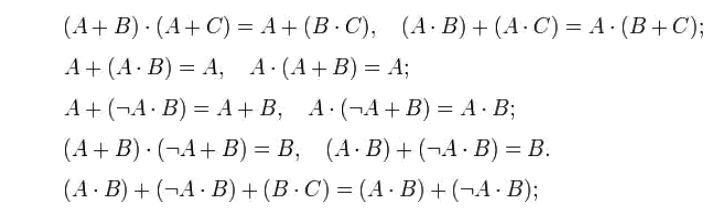
Related Topics