Circuit Families and Its Comparison

CIRCUIT FAMILIES AND ITS COMPARISON

The method of logical effort does not apply to arbitrary transistor networks, but only to logic gates. A logic gate has one or more inputs and one output, subject to the following restrictions:

The gate of each transistor is connected to an input, a power supply, or the output; and Inputs are connected only to transistor gates.

The first condition rules out multiple logic gates masquerading as one, and the second keeps inputs from being connected to transistor sources or drains, as in transmission gates without explicit drivers.

1. PSEUDO-NMOS Circuits

Static CMOS gates are slowed because an input must drive both NMOS and PMOS transistors.

In any transition, either the pullup or pulldown network is activated; meaning the input capacitance of the inactive network loads the input.

Moreover, PMOS transistors have poor mobility and must be sized larger to achieve comparable rising and falling delays, further increasing input capacitance.

Pseudo-NMOS and dynamic gates offer improved speed by removing the PMOS transistors from loading the input.

This section analyzes pseudo-NMOS gates, while section 10.2 explores dynamic logic. Pseudo-NMOS gates resemble static gates, but replace the slow PMOS pullup stack with a single grounded PMOS transistor which acts as a pullup resistor.

The effective pullup resistance should be large enough that the NMOS transistors can pull the output to near ground, yet low enough to rapidly pull the output high.

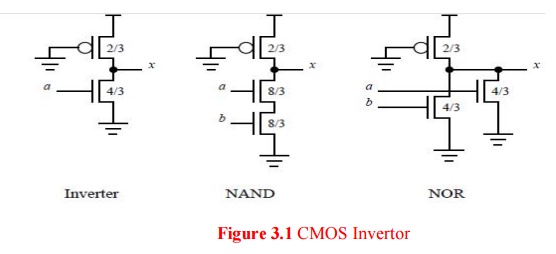
Figure shows several pseudo-NMOS gates ratioed such that the pulldown transistors are about four times as strong as the pullup.

The logical effort follows from considering the output current and input capacitance compared to the reference inverter from Figure Sized as shown, the PMOS transistors produce 1/3 of the current of the reference inverter and the NMOS transistor stacks produce 4/3 of the current of the reference inverter.

For falling transitions, the output current is the pulldown current minus the pullup current which is fighting the pulldown,For rising transitions, the output current is just the pullup current, 1/3.

The inverter and NOR gate have an input capacitance of 4/3. The falling logical effort is the input capacitance divided by that of an inverter with the same output current, or The rising logical effort is three times greater, because the current produced on a rising transition is only one third that of a falling transition. The average logical effort is g = (4=9+4=3)=2 = 8.

This neither is independent of the number of inputs, explaining why pseudo-NMOS is a way to build fast wide NOR gates. Table shows the rising, falling, and average logical efforts of other pseudo-NMOS gates, assuming _ = 2 and a 4:1 pulldown to pullup strength ratio.

Comparing this with Table shows that pseudo-NMOS multiplexers are slightly better than CMOS multiplexers and that pseudo-NMOS NAND gates are worse than CMOS NAND gates.

Since pseudo- NMOS logic consumes power even when not switching, it is best used for critical NOR functions where it shows greatest advantage.

Similar analysis can be used to compute the logical effort of other logic technologies, such as classic NMOS and bipolar and GaAs.

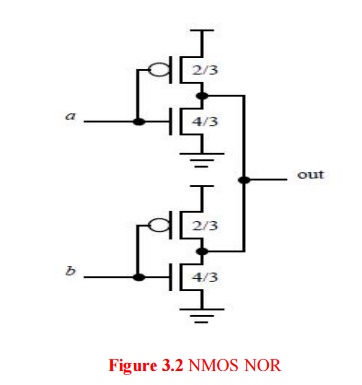
2. Symmetric NOR gates

Johnson proposed a novel structure for a 2-input NOR, shown in Figure. The gate consists of two inverters with shorted outputs, ratioed such that an inverter pulling down can overpower an inverter pulling up.

This ratio is exactly the same as is used for pseudo-NMOS gates. The difference is that when the output should rise, both inverters pull up in parallel, providing more current than is available from a regular pseudo-NMOS pullup.

The worst-case pulldowncurrent is equal to that of a unit inverter, as we had found in the analysis of pseudo-NMOS NOR gates. The pullup current comes from two PMOS transistors in parallel and is thus 2=3 that of a unit inverter. Therefore, the logical effort is 2=3 for a falling output and 1 for a rising output.

The average effort is g = 5=6, which is better than that of a pseudo-NMOS NOR and far superior to that of a static CMOS NOR and even for NAND gates.

3. Domino circuits

Pseudo-NMOS gates eliminate the bulky PMOS transistors loading the inputs, but pay the price of quiescent power dissipation and contention between the pullup and pulldown transistors.

Dynamic gates offer even better logical effort and lower power consumption by using a clocked precharge transistor instead of a pullup that is always conducting. The dynamic gate is precharged HIGH then may evaluate LOW through an NMOS stack.

Unfortunately, if one dynamic inverter directly drives another, a race can corrupt the result. When the clock rises, both outputs have been precharged HIGH.

The HIGH input to the first gate causes its output to fall, but the second gate’s output also falls in response to its initial HIGH input. The circuit therefore produces an incorrect result because the second output will never rise during evaluation, as shown in Figure.

Domino circuits solve this problem by using inverting static gates between dynamic gates so that the input to each dynamic gate is initially LOW.

The falling dynamic output and rising static output ripple through a chain of gates like a chain of toppling dominos.

Domino logic runs 1:5 to 2 times faster than static CMOS logic because dynamic gates present a much lower input capacitance for the same output current and have a lower switching threshold, and because the inverting static gate can be skewed to favor the critical monotonically rising evaluation edges.

Figure shows some domino gates. Each domino gate consists of a dynamic gate followed by an inverting static gate1.

The static gate is often but not always an inverter. Since the dynamic gate’s output falls monotonically during evaluation, the static gate should be skewed high to favor its monotonically rising output.

We have calculated the logical effort of high-skew gates in Table and will compute the logical effort of dynamic gates in the next section.

The logical effort of a domino gate is then the product of the logical effort of the dynamic gate and of the high-skew gate. Remember that a domino gate counts as two stages when choosing the best number of stages.

A dynamic gate may be designed with h or without a clocked evaluation transistor; the extra transistor slows the gate but eliminates any path between power and ground during p recharge when the inputs are still high.

Some dynamic gates include weak PMOS transistors called keepers so that the dynamic output will remain driven if the clock stops high. Domino designers face a number of questions when selecting a circuit topology.

How many stages should be used? Should the static gates be inverters, or should they perform logic? How should precharge transistors and keepers be sized? What is the benefit of removing the clocked evaluation transistors? We will show that domino logic should be designed with a stage effort of 2–2:75, rather than 4 that we found for static logic.

Therefore, paths tend to use more stages and it is rarely beneficial to perform logic with the inverting static gates.