Circuit Design of Latches and Flip Flops

CIRCUIT DESIGN OF LATCHES AND FLIP FLOPS:

Another class of logic circuits are sequential circuits. These circuits are two-valued networks in which the outputs at any instant are dependent not only upon the inputs present at that instant but also upon the past history (sequence) of inputs.

Sequential circuits are classified into:

§   Synchronous sequential circuits –Their behaviour is determined by the values of thesignals at only discrete instants of time.

§   Asynchronous  sequential circuits  –Their  behaviour  is  immediately affected by the input signal changes.

The block diagram of a sequential circuit is shown below:

The basic logic element that provides memory in many sequential circuits is the flip-flop.

1. Latches

Latches form one class of flip-flops. This class is characterized by the fact that the timing of the output changes is not controlled. Although latches are useful for storing binary information and for the design of asynchronous sequential circuits, they are not practical for use in synchronous sequential circuits.

2. The SR Latch

It is a circuit with two cross-coupled NOR gates or two cross-coupled NAND gates. The one with NOR gates is shown below:

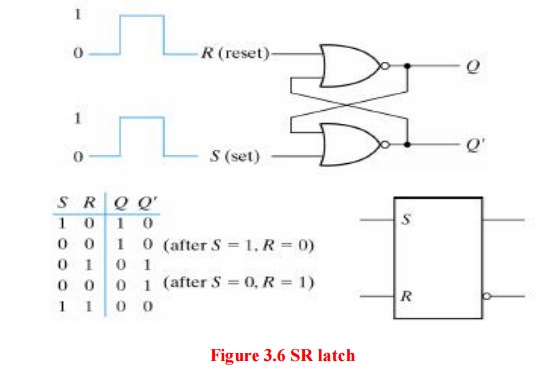
The condition that is undefined is when both inputs are equal to 0 at the same time. Comparing the NAND with the NOR latch note that the input signals for the NAND require the complement of those values used for the NOR latch.

Because the NAND latch requires a 0 signal to change its state, it is sometimes referred to as an S′-R′ latch. The operation of the SR latch can be modified to provide an additional control input that determines when the state of the latch can be changed.

An SR latch with control input is shown below: The control input C acts as an enable signal form the other two inputs.

An indeterminate condition occurs when all three inputs are equal to 1. This condition makes the circuit difficult to manage and is seldom used in practice.

Nevertheless, it is an important circuit because other latches and flip-flops are realized from it.

3. The Gated D Latch

One way to eliminate the undesirable condition of the indeterminate state in the SR latch is to ensure that inputs S and R are never equal to 1 at the same time. This is done by the D latch

4. Flip-Flops

When latches are used for the memory elements in sequential circuits, a serious difficulty arises. Recall that latches have the property of immediate output responses (i.e., transparency).

Because of this the output of a latch cannot be applied directly (or through logic) to the input of the same or another latch when all the latches are triggered by a common clock source. Flip -flops are used to overcome this difficulty.

5. Edge-Triggered D Flip-Flop

A D flip-flop may be realized with two D latches connected in a master-slave configuration: The circuit samples the D input and changes its Q output only at the negative-edge of the controlling clock signal (CLK).

It is also possible to design the circuit so that the flip-flop output changes on the positive edge of the clock (transition from 0 to 1).

This happens in a flipflop that has an additional inverter between the CLK terminal and the junction between the other inverter and input C on the master latch. An efficient realization of a positive edge-triggered D flip-flop uses three SR latches:

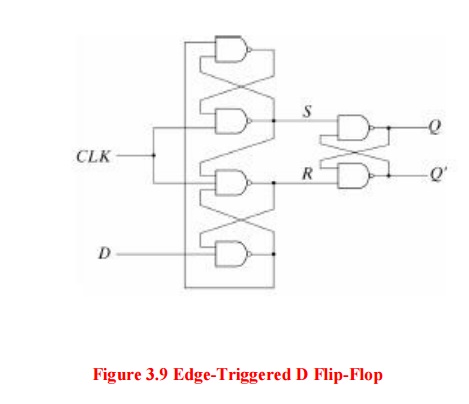
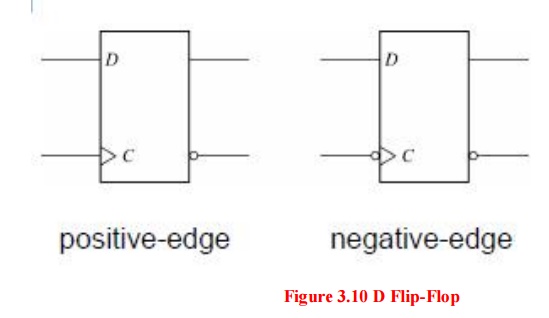
The graphic symbol for the edge-triggered D flipflop is:

6. Other Flip-Flops

The most economical and efficient flip-flop in terms of transistor count and silicon area is the D flip-flop. Other types of flip-flops can be realized by using the D flip-flop and external logic.

Two flipflops widely used in the design of digital systems are the JK and the T flip-flops. There are three operations that can be performed with a flip-flop: set it to 1, reset it to 0, complement its output. The JK flip-flop performs all three:

7. Characteristic Tables

A characteristic table defines the logical properties of a flip-flop by describing its operation in tabular form. The flip-flops characteristic tables are:

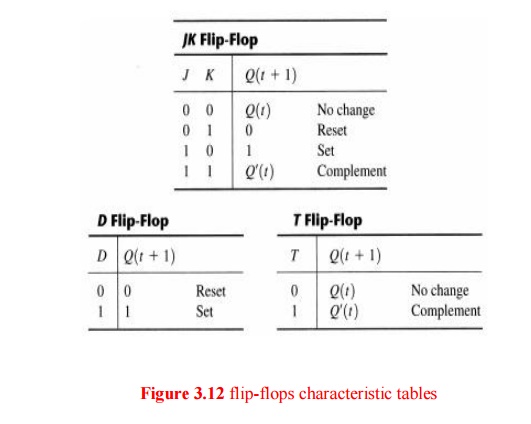
Q(t) refers to the present state prior to the application of a clock edge.

Q(t + 1) is the next state one clock period later. The clock edge input is not included in the characteristic tables, but is implied to occur between time t and t + 1.

8. Characteristic Equations

The logical properties of a flip-flop as described in its characteristic table can be expressed also algebraically with a characteristic equation. For the D flip-flop the characteristic equation is:

Q(t +1) = D

It states that the next state of the output will be equal to the value of input D in the present state.

The characteristic equation for the JK flip-flop is:

Q(t+1)=JQ’+K’Q

where Q is the value of the flip-flop output prior to the application of a clock edge. Finally, the characteristic equation for the T flipflop is:

Q(t+1)=TQ’+T’Q