Backward Difference operator(∇)

Backward Difference operator ( ∇) :

Let y = f(x) be a given function of x. Let y ₀ , y₁,..., y_n be the values of y at

x= x₀ , x₁ , x₂ ,..., x_n respectively. Then

y₁ − y₀ = ∇y₁

y ₂ − y₁ = ∇y₂

y _n − y_n−1 = ∇y_n

are called the first(backward) differences.

The operator ∇ is called backward difference operator and pronounced as nepla.

Second(backward) differences: ∇ ² y _n = ∇ y _n − ∇y_n+1 , n = 1,2,3,…

Third (backward) differences: ∇ ³ y _n = ∇ ² y_n − ∇² y_n−1 n = 1,2,3,…

In general, k^th (backward) differences: ∇ ^k y_n = ∇ ^{k −1} y_n − ∇^k−1 y_n−1 n = 1,2,3,…

Backward difference table:

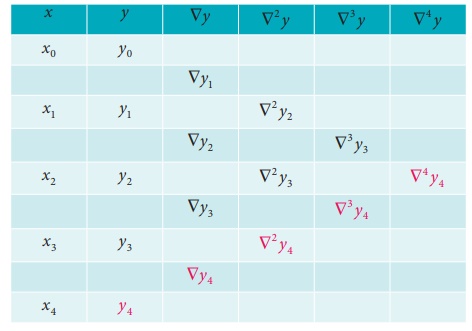
Backward differences can also be defined as follows.

∇ f (x) = f (x) − f (x − h)

First differences:  ∇ f (x + h) = f (x + h) − f (x)

∇ f (x + 2h) = f (x + 2h) − f (x + h),...,h is the interval of spacing.

Second differences:

∇ ² f (x + h) = ∇(∇f (x + h) = ∇( f (x + h) − f (x))

= ∇ f (x + h) − ∇f (x)

∇ ² f (x + 2h)         = ∇ f (x + 2h ) − ∇f (x + h)

Third differences:

∇ ³ f (x + h) = ∇ ² f (x + h ) − ∇² f (x)

∇ ³ f (x + 2h) = ∇ ² f (x + 2h ) − ∇² f (x + h)

Here we note that, ∇ f (x + h) = f (x + h ) − f (x) = Δf (x)

∇ f (x + 2h) = f (x + 2h ) − f (x + h) = Δf (x + h)

∇ ² f (x + 2h) = ∇ f (x + 2h ) − ∇f (x + h) = Δf (x + h ) − Δf (x)

= Δ² f (x)

In general, ∇ⁿ f (x + nh)= Δⁿ f (x)