Addition and Subtraction of Decimal Numbers

Operations on Decimal Numbers

Already we are familiar with decimal numbers. We know how to represent a decimal number as a fraction and the place values of digits. Now, let us learn the operations on decimal numbers.

Addition and Subtraction of Decimal Numbers

Iniya has purchased notebooks for ₹ 46.50 and a pencil box for ₹ 16.50. How much she will get as balance if she paid ₹ 100 to the shop keeper?

Price of a note book = ₹ 46.50 ; Price of a pencil box= ₹ 16.50

To find the amount to be paid, we have to add the price of both the items.

To get the balance amount we have to subtract the total expense from ₹ 100. To know the total expenses and the balance money, we need to understand addition and subtraction of decimals.

Addition and subtraction of decimals through models

Decimal grid or area models can be used to understand the process of addition and subtraction using decimal numbers.

(i) Grid model

We see below the grids to represent the decimal numbers 1.0, 0.1 and 0.01.

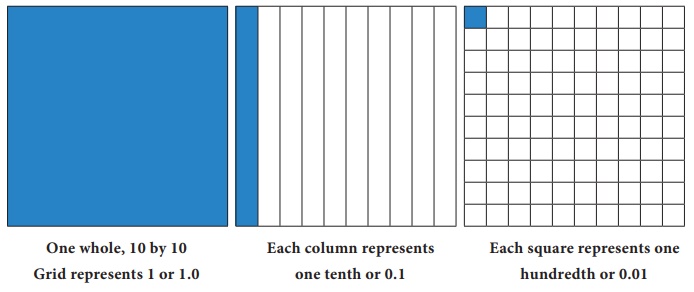
Having these grids let us try to do addition and subtraction of decimal numbers.

Example 1.5

 Find the sum of 0.16 and 0.77 using decimal grid models.

Solution

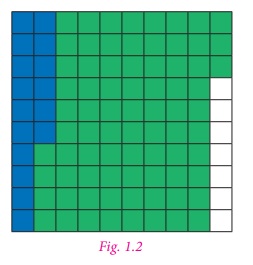
Here, 0.16= 16/100 and 0.77 = 77/100

First shade the region 0.16 and then shade 0.77.

The total shaded area is the sum.

So, 0.16 + 0.77 = 0.93 .

Example 1.6

Find 0.52 – 0.08 using decimal grid models.

Solution

Here 0.52 = 52 / 100and 0 .08 = 8/100. First shade the region 0.52 then cross out 0.08, which is 8/100 from the shaded area. The left out shaded region without cross marks is the difference. So, 0.52 − 0.08 = 0.44 .

Example 1.7

Find the value of 0.72 − 0.51 by using grids.

Solution

Take a square of 100 boxes. Shade 72 boxes to  represent 0.72.

Then strike out 51 boxes out of 72 shaded boxes to  subtract 0.51 from 0.72.

The left over shaded boxes represent the required value.

Therefore, 0.72 – 0.51 = 0.21.

Try this

Find the following using grid models:

(i) 0.83 + 0.04

Solution:

0.83= 83/100 and 0.04 = 4/100

Shading the regions

0.83 and 0.04

The sum is the total shaded region.

S = 0.83 + 0.04 = 0.87

(ii) 0.35 – 0.09

Solution:

0.35 = 35/100 and 0.09 = 9/100

Shading the regions 0.35 by shading 35 boxes out of 100. Striking off 9 boxes out of 35 shaded boxes to subtract 0.09 from 0.35.

The left over shaded boxes represent the required value.

0.35 - 0.09 = 0.26

(ii) Area model

 The whole number (unit place) which is a part of decimals represents a square area and 1/10 th part of this square area which is a thin rectangular  strip represents the tenth place of the decimal (0.1) and 1/100 ^th part of this  rectangular strip represents the hundredth place value (0.01) and the same process will be continued for the next place and so on.

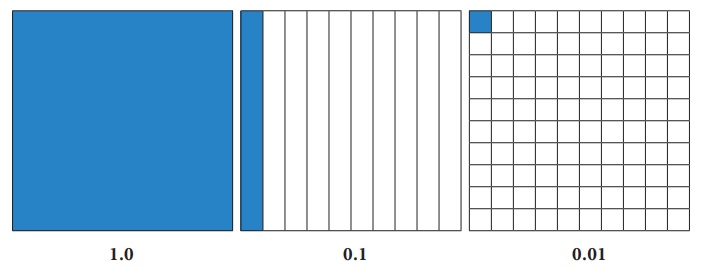
Having these square and rectangular area let us try to do addition and subtraction of decimal numbers.

Example 1.8

Add 3.2 + 6.4.

Solution

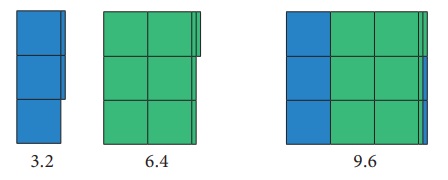
Here 3.2 is represented in Blue colour and 6.4 is represented in Green colour. Hence, the sum of 3.2 and 6.4 is 9.6.

Example 1.9

Subtract 7.5 – 3.4 .

Solution

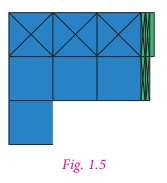
First represent the decimal number 7.5 using 7 squares and 5 rectangular strips. Cross out 3 squares from 7 squares and 4 rectangular strips from 5 rectangular strips to get the difference (see Fig. 1.5).

Hence, 7.5 – 3.4 = 4.1

Try this

Using the area models solve the following:

(i) 1.2 + 3.5

Solution:

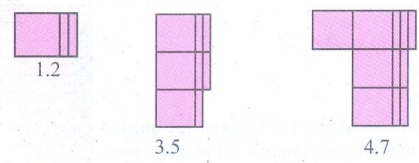
Here 1.2 is represented in blue colour and 3.5 is represented in Green colour. Sum of 1.2 and 3.5 is 4.7. 

(ii) 3.5 − 2.3

Solution:

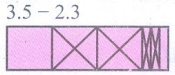
Representing 3.5 using 3 squares and 5 rectangular strips. Crossing out 2 squares from 3 squares and 3 rectangular strips from 5 to get the difference. So 3.5 - 2.3 = 1.2. 

(iii) Place value grid model

So far we have discussed grid models to do addition and subtraction of decimal numbers. Earlier we have studied representation of decimal numbers in place value tables. Let us use the same representation for addition and subtraction of decimal numbers.

For example, while adding 4.83 and 1.67, we have

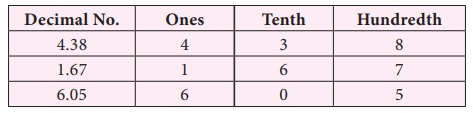
Therefore, 4.38 + 1.67 = 6.05.

Example 1.10

Add the following : (i) 30.9 + 52.73 (ii) 25.67 + 33.856

Solution

(i) 30.9 + 52.73

Let us use the place value grid.

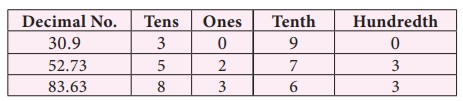
(Since the digits in the decimal place of 52.73 is 2 and 30.9 is 1, we should add 0 at the hundredth place of 30.9 to equalise the digits in the decimal place)

Therefore, 30.9 + 52.73 = 83.63.

(ii) 25.67 + 33.856

Let us use the place value grid.

Therefore, 25.67 + 33.856 = 59.526.

Note

Adding zeros at the right end of decimal digits will not change the value of the number.

Example 1.11

Everyday Malar travels 1.820 km by bus and 295 m by walk to reach the school. Find the distance of school from her house in km.

Solution

1000 m =1 km; 1 m = 1/1000 km

Hence, 295 m = 295/1000 km

                       = 0.295 km

Distance travelled by bus =1.820 km

Distance covered by walk = 0.295 km

Total distance = 1.820 + 0.295

                       =1.820 + 0.295

                        =2.115 km

Therefore, the school is situated at the distance of 2.115 km from her house.

Example 1.12

Subtract 2.85 from 4.97.

Solution

4.97 – 2.85 = ?

Let us use the place value grid.

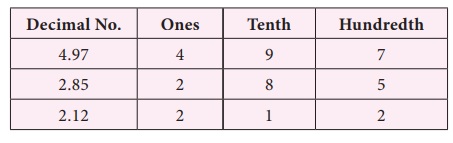
Therefore, 4.97 – 2.85 = 2.12.

Example 1.13

Subtract 3.09 from 12.7.

Solution

12.7 – 3.09 = ?

Let us use the place value grid.

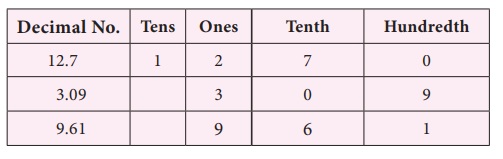
Therefore, 12.7 – 3.09 = 9.61.

Note

1. We can equalize the decimal digits of given numbers by adding zero at the right end of a decimal number that has only one decimal digit.

2. Zeros are added at the right end of decimal digits of a decimal number that are to be added or subtracted.

Example 1.14

Subtract 32.042 from 86.9.

Solution

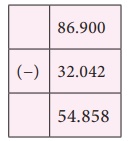
Therefore, 86.9 – 32.042 = 54.858.

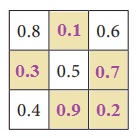
Try this

Complete the magic square in such a way that rows, columns and diagonals give the same sum 1.5.

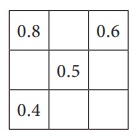
Solution

Example 1.15

Naren bought 7.4 kg of mangoes. On the way home, he gave 4.650 kg of mangoes to his sister’s family. Find the weight of the remaining mangoes.

Solution

 Mangoes bought by Naren = 7.4 kg

Mangoes given to Naren’s sister = 4.650 kg

Mangoes left for Naren’s family = 7.400 − 4.650

Weight of remaining mangoes = 2.750 kg

Therefore, the weight of the remaining mangoes is 2.750 kg.

We use decimals every day, while dealing with money, weight, length etc. Decimal numbers are used in situations where more accuracy is required.