Abstraction

Abstraction

To ride a bicycle, it is sufficient to understand the functioning of the pedal, handlebar, brakes and bell. As a rider, we model a bicycle by these four features. A bicycle has a lot more details, which the rider can ignore. Those details are irrelevant for the purpose of riding a bicycles.

A problem can involve a lot of details. Several of these details are irrelevant for solving the problem. Only a few details are essential. Abstraction is the process of ignoring or hiding irrelevant details and modeling a problem only by its essential features. In our everyday life, we use abstractions unconsciously to handle complexity. Abstraction is the most effective mental tool used for managing complexity. If we do not abstract a problem adequately, we may deal with unnecessary details and complicate the solution.

Example 6.9. A map is an abstraction of the things we find on the ground. We do not represent every detail on the ground. The map-maker picks out the details that we need to know. Different maps are drawn for different purposes and so use different abstractions, i.e., they hide or represent different features. A road map is designed for drivers. They do not usually worry about hills so most hills are ignored on a road map. A walker's map is not interested in whether a road is a one-way street, so such details are ignored.

Example 6.10. In medicine, different specialists work with different abstractions of human body. An orthopaedician works with the abstraction of skeletal system, while a gastroenterologist works with digestive system. A physiotherapist abstracts the human body by its muscular system.

We use abstraction in a variety of ways while constructing algorithms — in the specification of problems, representing state by variables, and decomposing an algorithm to functions. An algorithm designer has to be trained to recognize which features are essential to solve the problem, and which details are unnecessary. If we include unnecessary details, it makes the problem and its solution over-complicated.

Specification abstracts a problem by the properties of the inputs and the desired input-output relation. We recognize the properties essential for solving the problem, and ignore the unnecessary details.

State: In algorithms, the state of a computation is abstracted by a set of variables.

Functions: When an algorithm is very complex, we can decompose it into functions and abstract each function by its specification.

1. State

State is a basic and important abstraction. Computational processes have state. A computational process starts with an initial state. As actions are performed, its state changes. It ends with a final state. State of a process is abstracted by a set of variables in the algorithm. The state at any point of execution is simply the values of the variables at that point.

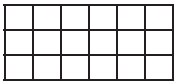
Example 6.11. Chocolate Bars: A rectangular chocolate bar is divided into squares by horizontal and vertical grooves. We wish to break the bar into individual squares.

To start with, we have the whole of the bar as a single piece. A cut is made by choosing a piece and breaking it along one of its grooves. Thus a cut divides a piece into two pieces. How many cuts are needed to break the bar into its individual squares?

In this example, we will abstract the essential variables of the problem. We solve the problem in Example 8.6.

Essential variables: The number of pieces and the number of cuts are the essential variables of the problem. We will represent them by two variables, p and c, respectively. Thus, the state of the process is abstracted by two variables p and c.

Irrelevant details:

1. The problem could be cutting a chocolate bar into individual pieces or cutting a sheet of postage stamps into individual stamps. It is irrelevant. The problem is simply cutting a grid of squares into individual squares.

2. The sequence of cuts that have been made and the shapes and sizes of the resulting pieces are irrelevant too. From p and c, we cannot reconstruct the sizes of the individual pieces. But, that is irrelevant to solving the problem

Example 6.12. Consider Example 1.2, Goat, grass and wolf problem. In this example,

we will write a specification of the problem. We will solve it in Example 2.1. The problem involves four individuals, and each is at one of the two sides of the river. This means that we can represent the state by four variables, and each of them has one of the two values. Let us name the variables farmer, goat, grass and wolf, and their possible values L and R. A value of L means "at the left side". A value of R means "at the right side". Since the boat is always with the farmer, it is important to not introduce a variable to represent its position.

In the initial state, all four variables farmer, goat, grass, wolf have the value L.

farmer, goat, grass, wolf = L, L, L, L

In the final state, all four variables should have the value R.

farmer, goat, grass, wolf = R, R, R, R

The specification of the problem is

cross_river

--inputs: farmer, goat, grass, wolf = L, L, L, L

--outputs: farmer, goat, grass, wolf = R, R, R, R

subject to the two constraints that

1. the goat cannot be left alone with the grass:

if goat = grass then farmer = goat

2. the goat cannot be left alone with the wolf:

if goat = wolf then farmer = goat

2. Assignment statement

Variables are named boxes to store values. Assignment statement is used to store a value in a variable. It is written with the variable on the left side of the assignment operator and a value on the right side.

variable := value

When this assignment is executed, the value on the right side is stored in the variable on the left side. The assignment

m := 2

stores value 2 in variable m.

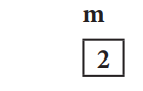
If the variable already has a value stored in it, assignment changes its value to the value on the right side. The old value of the variable is lost.

The right side of an assignment can be an expression.

variable := expression

In this case, the expression is evaluated and the value of the expression is stored in the variable. If the variable occurs in the expression, the current value of the variable is used in evaluating the expression, and then the variable is updated. For example, the assignment

m := m + 3

evaluates the expression m + 3 using the current value of m.

m + 3

= 2 + 3

= 5

and stores the value 5 in the variable m.

The two sides of an assignment statement are separated by the symbol :=, known as assignment operator, and read as "becomes" or "is assigned". The assignment statement

v := e

is read as v "becomes" e. Note that assignment operator is not equality operator¹. The meanings of v := e and v = e are different. Assignment does not state a mathematical equality of a variable, but changes the value of a variable. The assignment m := m + 3 does not state that m is equal to m + 3. Rather, it changes the value of the variable m to the value of the expression m + 3.

An assignment statement can change the values of multiple variables simultaneously. In that case, the number of variables on the left side should match the number of expressions on the right side. For example, if we wish to assign to three variables v1, v2 and v3, we need 3 expressions, say, el, e2, e3.

vl, v2, v3 := el, e2 , e3

The left side is a comma-separated list of variables. The right side is a comma-separated list of expressions. To execute an assignment statement, first evaluate all the expressions on the right side using the current values of the variables, and then store them in the corresponding variables on the left side.

Example 6.13. What are the values of variables m and n after the assignments in

line (1) and line (3)?

1.           m, n := 2 , 5

2.           m, n = ? , ?

3.           m,n:=m+3,n-1

4.           m, n = ? , ?

The assignment in line (1) stores 2 in variable m, and 5 in variable n.

The assignment in line (3) evaluates the expressions m + 3 and n - 1 using the current values of m and n as

m + 3 , n - 1

=2+3,5-1

= 5,4

and stores the values 5 and 4 in the variables m and n, respectively.

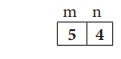
1. m, n := 2,5

2. -- m, n = 2 , 5

3. m, n := m + 3, n - 1

4. -- m, n = 2 + 3, 5-1 = 5, 4

Values of the variables after the two assignments are shown in in line (2) and line(4).

Example 6.14. In Example 6.11, we abstracted the state of the process by two variables p and c. The next step is to model the process of cutting the chocolate bar. When we make a single cut of a piece, the number of pieces (p) and the number of cuts  both increase by 1. We can model it by an assignment statement.

p, c := p + 1, c+1

which is read as p and c "become" p + 1 and c + 1, respectively.