Specification

Specification

To solve a problem, first we must state the problem clearly and precisely. A problem is specified by the given input and the desired output. To design an algorithm for solving a problem, we should know the properties of the given input and the properties of the desired output. The goal of the algorithm is to establish the relation between the input and the desired output.

An algorithm is specified by the properties of the given input and the relation between the input and the desired output. In simple words, specification of an algorithm is the desired input-output relation.

The inputs and outputs are passed between an algorithm and the user through variables. The values of the variables when the algorithm starts is known as the initial state, and the values of the variables when the algorithm finishes is known as the final state.

Let P be the required property of the inputs and Q the property of the desired outputs. Then the algorithm S is specified as

1.    algorithm_name (inputs)

2.    inputs : P

3.    outputs: Q

This specification means that if the algorithm starts with inputs satisfying P, then it will finish with the outputs satisfying Q.

A double dash -- indicates that the rest of the line is a comment. Comments are statements which are used to annotate a program for the human readers and not executed by the computer. Comments at crucial points of flow are useful, and even necessary, to understand the algorithm. In our algorithmic notation, we use double dashes (—) to start a comment line. (In C++, a double slash // indicates that the rest of the line is a comment).

Example 6.6. Write the specification of an algorithm to compute the quotient and remainder after dividing an integer A by another integer B. For example,

divide (22, 5) = 4, 2

divide (15, 3) = 5 , 0

Let A and B be the input variables. We will store the quotient in a variable q and the remainder in a variable r. So q and r are the output variables.

What are the properties of the inputs A and B?

1.    A should be an integer. Remainder is meaningful only for integer division, and

2.    B should not be 0, since division by 0 is not allowed.

We will specify the properties of the inputs as

— inputs: A is an integer and B ≠ 0

What is the desired relation between the inputs A and B, and the outputs q and r?

1. The two outputs q (quotient) and r (remainder) should satisfy the property

A = q X B + r, and

2. The remainder r should be less than the divisor B,

0 ≤ r < B

Combining these requirements, we will specify the desired input-output relation as

— outputs: A = q X B + r and 0 < r < B.

The comment that starts with — inputs: actually is the property of the given inputs. The comment that starts with — outputs: is the desired relation between the inputs and the outputs. The specification of the algorithm is

1. divide (A , B)

2. -- inputs: A is an integer and B ≠ 0

3. -- outputs : A = q X B + r and 0 ≤ r < B

Specification format: We can write the specification in a standard three part format:

•      The name of the algorithm and the inputs.

•      Input: the property of the inputs.

•      Output: the desired input-output relation.

The first part is the name of the algorithm and the inputs. The second part is the property of the inputs. It is written as a comment which starts with — inputs: The third part is the desired input-output relation. It is written as a comment which starts with — outputs:. The input and output can be written using English and mathematical notation.

Example 6.7. Write the specification of an algorithm for computing the square root of a number.

1.    Let us name the algorithm square_root.

2.    It takes the number as the input. Let us name the input n. n should not be negative.

3.    It produces the square root of n as the output. Let us name the output y. Then n should be the square of y.

Now the specification of the algorithm is

square_root(n)

-- inputs: n is a real number, n ≥ 0.

-- outputs: y is a real number such that y ²= n. 

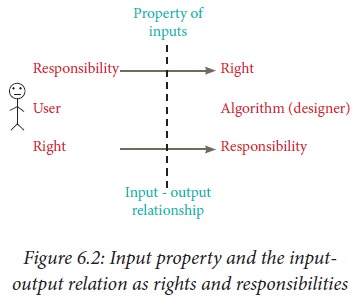
Specification as contract

Specification of an algorithm serves as a contract between the designer of the algorithm and the users of the algorithm, because it defines the rights and responsibilities of the designer and the user.

Ensuring that the inputs satisfy the required properties is the responsibility of the user, but the right of the designer. The desired input-output relation is the responsibility of the designer and the right of the user. Importantly, if the user fails to satisfy the properties of the inputs, the designer is free from his obligation to satisfy the desired input-output relation.

Example 6.8. Consider the specification of the algorithm square_root.

square_root(n)

-- inputs: n is a real number, n ≥ 0.

-- outputs : y is a real number such that y² = n.

The algorithm designer can assume that the given number is non-negative, and construct the algorithm. The user can expect the output to be the square root of the given number.

The output could be the negative square root of the given number. The specification did not commit that the output is the positive square root. If the user passes a negative number as the input, then the output need not be the square root of the number.