Transient Response Analysis

TRANSIENT RESPONSE ANALYSIS

(Dynamic Response/Time-History Analysis)

Structure response to arbitrary, time-dependent loading.

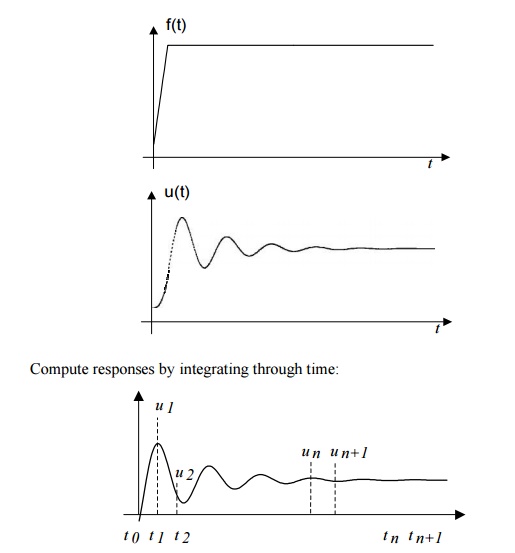
Compute responses by integrating through time:

B. Modal Method

First, do the transformation of the dynamic equations using the modal matrix before the time marching:

Then, solve the uncoupled equations using an integration method. Can use, e.g., 10%, of the total modes (m= n/10).

Uncoupled system, Fewer equations,

No inverse of matrices,

More efficient for large problems.

1Cautions in Dynamic Analysis

Symmetry: It should not be used in the dynamic analysis (normal modes, etc.) because symmetric structures can have antisymmetric modes.

Mechanism, rigid body motion means = 0. Can use this to check FEA models to see if they are properly connected and/or supported.

Input for FEA: loading F(t) or F( ) can be very complicated in real applications and often needs to be filtered first before used as input for FEA.

Examples

Impact, drop test, etc.

PROBLEM

In the spring structure shown k1 = 10 lb./in., k2 = 15 lb./in., k3 = 20 lb./in., P= 5 lb. Determine the deflection at nodes 2 and 3.

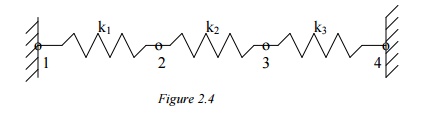
Solution:

Again apply the three steps outlined previously.

Step 1: Find the Element Stiffness Equations

Element 1:

Step 2: Find the Global stiffness matrix

Now the global structural equation can be written as above.

Step 3: Solve for Deflections

The known boundary conditions are: u1 = u4 = 0, F3 = P = 3lb. Thus, rows and columns 1 and 4 will drop out, resulting in t following matrix equation,

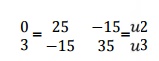
Solving, we get     u2 = 0.0692 & u3 = 0.1154    

PROBLEM                            

In the spring structure shown, k1 = 10 N/mm, k2 = 15 N/mm, k3 = 20 N/mm, k4 = 25 N/mm, k5 = 30 N/mm, k6 = 35 N/mm. F2 = 100 N. Find the deflections in all springs.

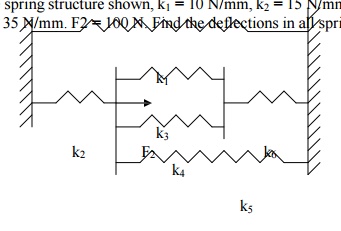
Solution:

Here again, we follow the three-step approach described earlier, without specifically mentioning at each step.

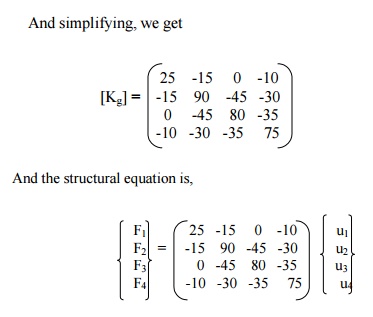
Now, apply the boundary conditions, u1 = u4 = 0, F2 = 100 N. This is carried out by deleting the rows 1 and 4, columns 1 and 4, and replacing F2 by 100N. The final matrix equation is,

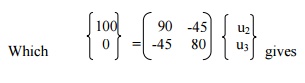
Deflections:                                                         

Spring 1:              u4 – u1       = 0                       

Spring 2:              u2 – u1       = 1.54590            

Spring 3:              u3 – u2       = -0.6763            

Spring 4:              u3      – u2   = -0.6763            

Spring 5:              u4      – u2   = -1.5459            

Spring 6:              u4      – u3   = -0.8696