Chapter: Mechanical : Finite Element Analysis : Dynamic Analysis Using Element Method
Consistent Mass Matrices
CONSISTENT MASS MATRICES
Natural frequencies and modes
Frequency response ( F(t)=Fo sinwt) Transient
response (F(t) arbitrary)
1 Single DOF System

Free Vibration:
f(t) = 0 and no damping (c = 0) Eq. (1) becomes
mu ku
(meaning: inertia force + stiffness force = 0) Assume:

This is the circular natural frequency of the single DOF system (rad/s). The cyclic frequency (1/s = Hz) is

2.Multiple DOF System
Equation of Motion
Equation of motion for the whole structure is
Mu Cu Ku f (t) , (8)
in which: u nodal displacement vector,
M mass matrix,
C damping matrix,
K stiffness matrix, f forcing vector.
Physical meaning of Eq. (8):
Inertia forces + Damping forces + Elastic forces
= Applied forces
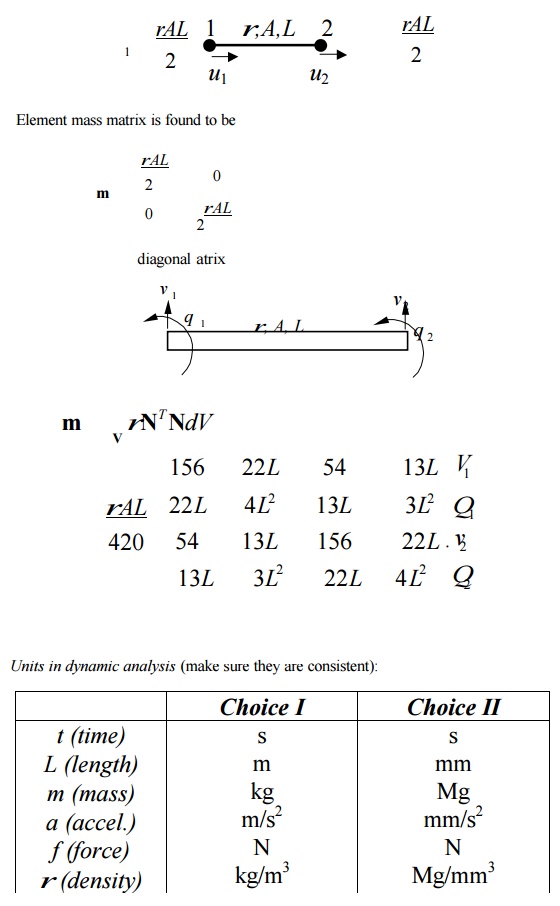
Mass Matrices
Lumped mass matrix (1-D bar element):
VECTOR ITERATION METHODS
Study of the dynamic characteristics of a structure: natural frequencies normal modes shapes)
Let f(t) = 0 and C = 0 (ignore damping) in the dynamic equation (8) and obtain
Mu Ku 0
Assume that displacements vary harmonically with time, that is,
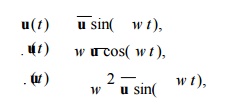
where u is the vector of nodal displacement amplitudes.
Eq. (12) yields,

This is a generalized eigenvalue problem (EVP).
Solutions?
This is an n-th order polynomial of from which we can find n solutions (roots) or eigenvalues
i (i = 1, 2, …, n) are the natural frequencies (or characteristic frequencies) of the structure (the smallest one) is called the fundamental frequency. For each gives one
solution (or eigen) vector

if wi wj . That is, modes are orthogonal (or independent) to each other with respect to K and
M matrices.
Note:
Magnitudes of displacements (modes) or stresses in normal mode analysis have no physical meaning.
For normal mode analysis, no support of the structure is necessary.
i = 0 there are rigid body motions of the whole or a part of the structure. apply this to check
the FEA model (check for mechanism or free elements in the models).
Lower modes are more accurate than higher modes in the FE calculations (less spatial variations in the lower modes fewer elements/wave length are needed).
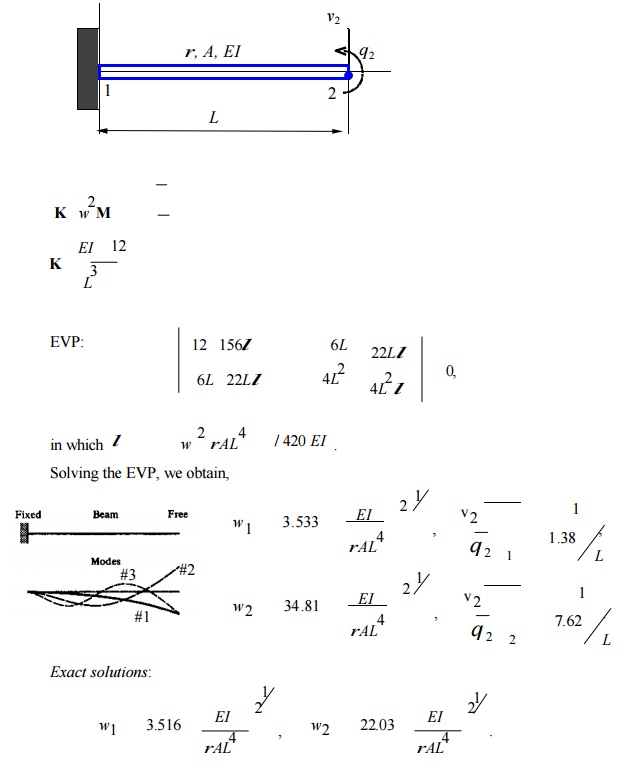
Example:
Related Topics