Schmitt Trigger

Schmitt Trigger

Sometimes an input signal to a digital circuit doesn't directly fit the description of a digital signal. For various reasons it may have slow rise and/or fall times, or may have acquired some noise that could be sensed by further circuitry. It may even be an analog signal whose frequency we want to measure. All of these conditions, and many others, require a specialized circuit that will "clean up" a signal and force it to true digital shape.

The required circuit is called a Schmitt Trigger. It has two possible states just like other multivibrators. However, the trigger for this circuit to change states is the input voltage level, rather than a digital pulse. That is, the output state depends on the input level, and will change only as the input crosses a pre- defined threshold.

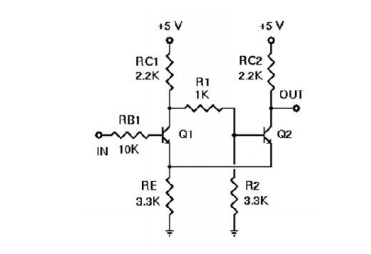
Unlike the other multivibrators you have built and demonstrated, the Schmitt Trigger makes its feedback connection through the emitters of the transistors as shown in the schematic diagram to the right. This makes for some useful possibilities, as we will see during our discussion of the operating theory of this circuit.

To understand how this circuit works, assume that the input starts at ground, or 0 volts. Transistor Q1 is necessarily turned off, and has no effect on this circuit. Therefore, RC1, R1, and R2 form a voltage divider across the 5 volt powersupply to set the base voltage of Q2 to a value of (5 × R2)/(RC1 + R1 + R2). Ifwe assume that the two transistors are essentially identical, then as long as the input voltage remains significantly less than the base voltage of Q2, Q1 will remain off and the circuit operation will not change.

While Q1 is off, Q2 is on. Its emitter and collector current are essentially the same, and are set by the value of RE and the emitter voltage, which will be less than the Q2 base voltage by V_BE. If Q2 is in saturation under these circumstances, the output voltage will be within a fraction of the threshold voltage set by RC1, R1, and R2. It is important to note that the output voltage of this circuit cannot drop to zero volts, and generally not to a valid logic 0. We can deal with that, but we must recognize this fact.

Now, suppose that the input voltage rises, and continues to rise until it approaches the threshold voltage on Q2's base. At this point, Q1 begins to conduct. Since it now carries some collector current, the current through RC1 increases and the voltage at the collector of Q1 decreases. But this also affects our voltage divider, reducing the base voltage on Q2. But since Q1 is now conducting it carries some of the current flowing through RE, and the voltage across RE doesn't change as rapidly. Therefore, Q2 turns off and the output voltage rises to +5 volts. The circuit has just changed states.

If the input voltage rises further, it will simply keep Q1 turned on and Q2 turned off. However, if the input voltage starts to fall back towards zero, there must clearly be a point at which this circuit will reset itself. The question is, What is the falling threshold voltage? It will be the voltage at which Q1's base becomes more negative than Q2's base, so that Q2 will begin conducting again. However, it isn't the same as the rising threshold voltage, since Q1 is currently affecting the behavior of the voltage divider.

We won't go through all of the derivation here, but when V_IN becomes equal to Q2's base voltage, Q2's base voltage will be:

As V_IN approaches this value, Q2 begins to conduct, taking emitter current away from Q1. This reduces the current through RC1 which raises Q2's base voltage further, increasing Q2's forward bias and decreasing Q1's forward bias. This in turn will turn off Q1, and the circuit will switch back to its original state.

Three factors must be recognized in the Schmitt Trigger. First, the circuit will change states as V_IN approaches V_B2, not when the two voltages are equal. Therefore V_B2 is very close to the threshold voltage, but is not precisely equal to it. For example, for the component values shown above, V_B2 will be 2.54 volts when Q1 is held off, and 2.06 volts as V_IN is falling towards this value.

Second, since the common emitter connection is part of the feedback system in this circuit, RE must be large enough to provide the requisite amount of feedback, without becoming so large as to starve the circuit of needed current. If RE is out of range, the circuit will not operate properly, and may not operate as anything more than a high-gain amplifier over a narrow input voltage range, instead of switching states.

The third factor is the fact that the output voltage cannot switch over logic levels, because the transistor emitters are not grounded. If a logic-level output is required, which is usually the case, we can use a circuit such as the one shown here to correct this problem. This circuit is basically two RTL inverters, except that one uses a PNP transistor. This works because when Q2 above is turned off, it will hold a PNP inverter off, but when it is on, its output will turn the PNP transistor on. The NPN transistor here is a second inverter to re-invert the signal and to restore it to active pull-down in common with all of our other logic circuits.

The circuit you will construct for this experiment includes both of the circuits shown here, so that you can monitor the response of the Schmitt trigger with L0.

Schmitt Waveform Generators

Simple Waveform Generators can be constructed using basic Schmitt trigger action Inverters such as the TTL 74LS14. This method is by far the easiest way to make a basic astable waveform generator. When used to produce clock or timing signals, the astable multivibrator must produce a stable waveform that switches quickly between its "HIGH" and "LOW" states without any distortion or noise, and Schmitt inverters do just that.

We know that the output state of a Schmitt inverter is the opposite or inverse to that of its input state, (NOT Gate principles) and that it can change state at different voltage levels giving it "hysteresis". Schmitt inverters use a Schmitt Trigger action that changes state between an upper and a lower threshold level as the input voltage signal increases and decreases about the input terminal. This upper threshold level "sets" the output and the lower threshold level"resets" the output which equates to a logic "0" and a logic "1" respectively for an inverter. Consider the circuit below.

TTL Schmitt Waveform Generator

The circuit consists simply of a TTL 74LS14 Schmitt inverter logic gate with a capacitor, C connected between its input terminal and ground, (0v) with the positive feedback required for the circuit to oscillate is provided by the feedback resistor, R. So how does it work?. Assume that the charge across the capacitors plates is below the Schmitt's lower threshold level of 0.8 volt (Datasheet value). This therefore makes the input to the inverter at a logic "0" level resulting in a logic "1" output level (inverter principals). One side of the resistor R is now connected to the logic "1" level (+5V) output while the other side of the resistor is connected to the capacitor, C which is at a logic "0" level (0.8v or below).

The capacitor now starts to charge up in a positive direction through the resistor at a rate determined by the RC time constant of the combination. When the charge across the capacitor reaches the 1.6 volt upper threshold level of the Schmitt trigger (Datasheet value) the output from the Schmitt inverter changes rapidly from a logic level "1" to a logic level "0" state and the current flowing through the resistor changes direction.

This change now causes the capacitor that was originally charging up through the resistor, R to begin to discharge itself back through the same resistor until the charge across the capacitors plates reaches the lower threshold level of 0.8 volts and the inverters output switches state again with the cycle repeating itself over and over again as long as the supply voltage is present.

So the capacitor, C is constantly charging and discharging itself during each cycle between the upper and lower threshold levels of the Schmitt inverter producing a logic level "1" or a logic level "0" at the inverters output. However, the output square wave signal is not symmetrical producing a duty cycle of about 33% or 1/3 as the mark-to-space ratio between "HIGH" and "LOW" is 1:2 respectively due to the input gate characteristics of the TTL inverter.

The value of the feedback resistor, R MUST also be kept low to below 1kΩ_{for the circuit to} oscillate correctly, 220R to 470R is good, and by varying the value of the capacitor, C to vary the frequency. Also at high frequency levels the output waveform changes shape from a square shaped waveform to a trapezoidal shaped waveform as the input characteristics of the TTL gate are affected by the rapid charging and discharging of the capacitor.

With a resistor value between: 100R to 1kΩ, and a capacitor value of between: 1nF to 1000uF. This would give a frequency range of between 1Hzto 1MHz, (high frequencies produce waveform distortion).