Chapter: Automation, Production Systems, and Computer Integrated Manufacturing : Manufacturing Operations
Product/Production Relationships
PRODUCT/PRODUCTION
RELATIONSHIPS
Companies organize their manufacturing
operations and production systems as a function of the particular products they
make. It is instructive to recognize that there are certain product parameters
that are influential in determining how the products are manufactured. Let us
consider four key parameters: (1) production quantity, (2) product variety, (3)
complexity of assembled products, and (4) complexity of individual parts.
1
Production Quantity and Product Variety
We previously discussed production quantity and
product variety in Chapter 1 (Section 1.1). Let us develop a set of symbols to
represent these important parameters. First, let Q=production quantity and
P=product variety. Thus we can discuss product variety and production quantity
relationships as PQ relationships.
Q refers to the number of
units of a given part or product that are produced annually by a plant. Our
interest includes both the quantities of each individual part or product style
and the total quantity of all styles. Let us identify each part or product
style by using the subscript j, so that Qj=annual
quantity of style j. Then let Qf=total
quantity of all parts or products made in the factory. Qj and Qf
are related as follows:

where P=total number of different part or
product styles, and j is a subscript to identify products, j=1, 2, p , P.
P refers to the different product designs or types that are produced in a plant. It is a parameter that can be counted, and yet we recognize that the difference between products can be great or small. In Chapter 1, we distinguished between hard product variety and soft product variety. Hard product variety is when the products differ substantially. Soft product variety is when there are only small differences between products. Let us divide the parameter P into two levels, as in a tree structure. Call them P1 and P2. P1 refers to the number of distinct product lines produced by the factory, and P2 refers to the number of models in a product line. P1 represents hard product variety, and P2 is for soft variety.

2
Product and Part Complexity
How complex is each product made in the plant?
Product complexity is a complicated issue. It has both qualitative and
quantitative aspects. Let us deal with it using quantitative measures. For an
assembled product, one possible indicator of product complexity is its number of components—the more parts, the
more complex the product is. This is easily demonstrated by comparing the
numbers of components in various assembled products, as in Table 2.4. Our list
demonstrates that the more components a product has, the more complex it tends
to be.
For a fabricated component, a
possible measure of part complexity
is the number of processing steps required to produce it. An integrated
circuit, which is technically a monolithic silicon chip with localized
alterations in its surface chemistry, requires hundreds of processing steps in
its fabrication. Although it may measure only 9 mm (3 8 inch) on a side and is
0.5 mm (0.020 inch) thick, its complexity is orders of magnitude greater than a
round washer of 9 mm (3 8 inch) outside diameter, stamped out of 0.80mm (1
32inch) thick stainless steel in one step. In Table 2.5, we have compiled a
list of manufactured parts with the typical number of processing operations
that would be required for each.
So, we have complexity of an
assembled product defined as the number of distinct components; let np=
the number of parts per product. And we have processing complexity of each part
as the number of operations required to make it; let no= the number
of operations or processing steps to make a part.We can draw some distinctions
among production plants on the basis of np and no.As
defined in Table 2.6, three different types of plant can be identified: parts
producers, pure assembly plants, and vertically integrated plants.
TABLE 2.4 Typical Number of Separate Components in
Various Assembled Products (Compiled from [2], [4], and Other Sources)


Let us develop some simple
relationships among the parameters P, Q, np, and no that
indicate the level of activity in a manufacturing plant.We will ignore the
differences between P1 and P2 here. The total number of products made annually
in a plant is the sum of the quantities of the individual product designs, as
expressed in previous Eq. (2.1). Assuming that the products are all assembled
and that all component parts used in these products are made in the plant (no
purchased components), then the total number of parts manufactured by the plant
per year is given by:

where npf=total
number of parts made in the factory (pc yr), Qj=annual quantity of product style j (products yr), and
npj=number of parts in product j (pc product).
Finally, if all parts are
manufactured in the plant, then the total number of processing operations
performed by the plant is given by:

where nof=total number of operation
cycles performed in the factory (ops yr), and nojk=number of
processing operations for each part k, summed over the number of parts in
product j, npj. Parameter nof provides a numerical value
for the total activity level in the factory.
We might try to simplify this
to better conceptualize the situation by assuming that the number of product
designs P are produced in equal quantities Q, all products have the same number
of components np, and all components require an equal number of
processing steps no. In this case, the total number of product units
produced by the factory is given by:

The total number of parts
produced by the factory is given by:

And the total number of
manufacturing operation cycles performed by the factory is given by:

Using these simplified
equations, consider the following example.
EXAMPLE 2.2 A Manufacturing Operations (and Production Systems) Problem
Suppose a company has designed a new product
line and is planning to build a new plant to manufacture this product line. The
new line consists of 100 different product types, and for each product type the
company wants to produce 10,000 units annually. The products average 1000
components each, and the average number of processing steps required for each
component is 10. All parts will be made in the factory. Each processing step
takes an average of 1 min. Determine: (a) how many products, (b) how many
parts, and (c) how many production operations will be required each year, and
(d) how many workers will be needed for the plant, if it operates one shift for
250 day yr?
Solution: The total number of
units to be produced by the factory is given by Eq (2.5):
Q=PQ=100*10,000=1,000,000 products annually.
The total number of parts produced is:
npf=PQnp=1,000,000*1000=1,000,000,000 parts annually.
The number of distinct production operations
is:
nof=PQnpno=1,000,000,000*10=10,000,000,000 operations.
Let us try to estimate the number of workers
required. First consider the total time to perform these operations. If each
operation takes 1 min (1 60 hr),
Total time=10,000,000,000*1 60=166,666,667 hr
If each worker works 2000 hr
yr (40 hr wk*50 wk yr), then the total number of workers required is:
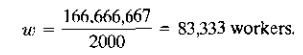
The factory in our example is
a fully integrated factory. It would be a big factory. The number of workers we
have calculated only includes direct labor. Add indirect labor, staff, and
management, and the number increases to well over 100,000 employees. Imagine
the parking lot. And inside the factory, the logistics problems of dealing with
all of the products, parts, and operations would be overwhelming. No
organization in its right mind would consider building or operating such a
plant today—not even the federal government.
3
Limitations and Capabilities of a Manufacturing
Plant
Companies do not attempt the kind of factory in
our example. Instead, today’s factory is designed with a much more specific
mission. Referred to as a focused factory
[5], it is a plant which concentrates “on a limited, concise, manageable set of
products, technologies, volumes, and markets.” It is a recognition that a
manufacturing plant cannot do everything. It must limit its mission only to a
certain scope of products and activities in which it can best compete. Its size
is typically limited to about 500 workers, although that number may vary widely
for different types of products and manufacturing operations.
Let us consider how a plant,
or its parent company, limits the scope of its manufacturing operations and
production systems. In limiting its scope, the plant in effect makes a set of
deliberate decisions about what it will not try to do. Certainly one way to
limit a plant’s scope is by avoiding being a fully integrated factory, at least
to the extent of our Example 2.2. Instead, it specializes in being either a
parts producer or an assembly plant. Just as it decides what it will not do,
the plant must also decide on the specific technologies, products, and volumes
in which it will specialize. These decisions define the plant’s intended
manufacturing capability. Manufacturing
capability refers to the technical and physical limitations of a
manufacturing firm and each of its plants. We can identify several dimensions
of this capability: (1) technological processing capability, (2) physical size
and weight of product, and (3) production capacity.
Technological
Processing Capability. The
technological processing capability of a plant (or company) is its available set of manufacturing
processes. Certain plants perform machining operations, others roll steel
billets into sheet stock, and others build automobiles. A machine shop cannot
roll steel, and a rolling mill cannot build cars. The underlying feature that
distinguishes these plants is the set of processes they can perform.
Technological processing capability is closely related to the material being
processed. Certain manufacturing processes are suited to certain materials,
while other processes are suited to other materials. By specializing in a certain
process or group of processes, the plant is simultaneously specializing in a
certain material type or range of materials.
Technological processing capability includes
not only the physical processes, but also the expertise possessed by plant
personnel in these processing technologies. Companies are limited by their
available processes. They must focus on designing and manufacturing products
for which their technological processing capability provides a competitive
advantage.
Physical
Product Limitations. A second
aspect of manufacturing capability is imposed by the physical product. Given a
plant with a certain set of processes, there are size and weight limitations on
the products that can be accommodated in the plant. Big, heavy products are
difficult to move. To move products about, the plant must be equipped with
cranes of large load capacity. Smaller parts and products made in large
quantities can be moved by conveyor or fork lift truck.The limitation on
product size and weight extends to the physical capacity of the manufacturing
equipment as well. Production machines come in different sizes. Larger machines
can be used to process larger parts. Smaller machines limit the size of the
work that can be processed. The set of production equipment, material handling,
storage capability, and plant size must be planned for products that lie within
a certain size and weight range.
Production
Capacity. A third limitation on a
plant’s manufacturing capability is the production quantity that can be produced in a given time period
(e.g., month or year). This quantity limitation is commonly called plant capacity, or production capacity, which is defined as the maximum rate of
production per period that a plant can achieve under assumed operating
conditions. The operating conditions refer to number of shifts per week, hours
per shift, direct labor manning levels in the plant, and similar conditions
under which the plant has been designed to operate. These factors represent
inputs to the manufacturing plant. Given these inputs, how much output can the
factory produce?
Plant capacity is often
measured in terms of output units, such as annual tons of steel produced by a
steel mill, or number of cars produced by a final assembly plant. In these
cases, the outputs are homogeneous, more or less. In cases where the output
units are not homogeneous, other factors may be more appropriate measures, such
as available labor hours of productive capacity in a machine shop that produces
a variety of parts.
Related Topics