Dynamic Analysis Using Element Method

DYNAMIC ANALYSIS USING ELEMENT METHOD

INTRODUCTION

It provides the basic equations necessary for structural dynamical analysis and developed both the lumped and the consistent mass matrix involved in the analysis of bar beam and spring elements.

1 Fundamentals of Vibration

Any motion which repeats itself after an interval of time is called vibration or oscillation or periodic motion

All bodies possessing mass and elasticity are capable of producing vibration.

2 Causes of Vibrations

o   Unbalanced forces in the machine. These force are produced from within the machine itself

o  Elastic nature of the system.

o Self excitations produced by the dry friction between the two mating surfaces. o External excitations applied on the system.

o  Wind may causes vibrations

o   Earthquakes may causes vibrations

3.Types of Vibrations

1.According to the actuating force

Free or natural vibrations

Forced vibrations

Damped vibrations

Undamped vibrations

2.According to motion of system with respect to axis

Longitudinal vibrations

Transverse vibrations

Torsional vibrations

EQUATION OF MOTION

There is two types of equation of motion

Longitudinal vibration of beam or axial vibration of a rod

Transverse vibration of a beam

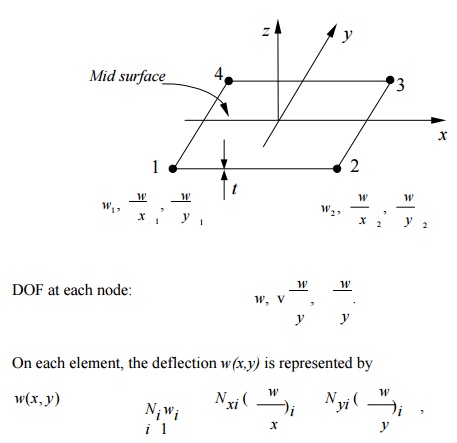
where N_i, N_xi and N_yi are shape functions. This is an incompatible element! The stiffness matrix is still of the form

k =   B^TEBdV ,

where B is the strain-displacement matrix, and E the stress- strain matrix.

Minding Plate Elements:

4-Node Quadrilateral

8-Node Quadrilateral

Three independent fields.

Deflection w(x,y) is linear for Q4, and quadratic for Q8.

Discrete Kirchhoff Element:

Triangular plate element (not available in ANSYS). Start with a 6-node riangular element,

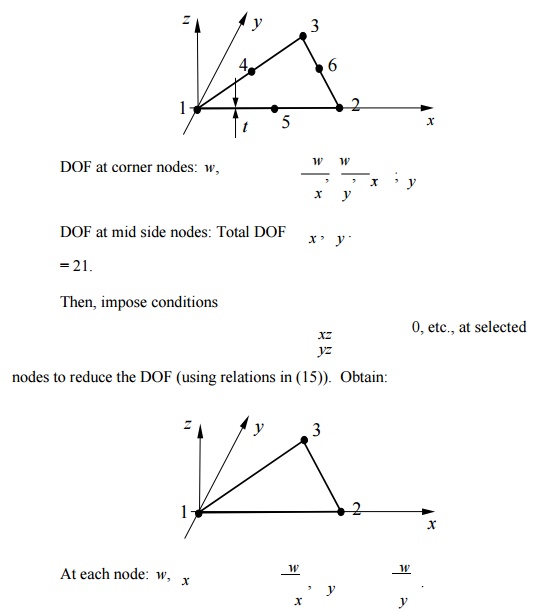
Total DOF = 9  (DKT Element).

Incompatible w(x,y);  convergence is faster (w is cubic along each edge) and it is efficient.

Test Problem:

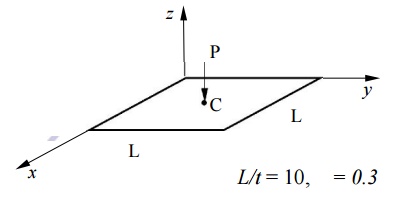
L/t = 10,   = 0.3

ANSYS 4-node quadrilateral plate element.

ANSYS Result for w_c

Mesh           wc (  PL²/D)

2        2                           0.00593

4        4                           0.00598

8        8                           0.00574

16      16                         0.00565

          :                            :

Exact Solution                         0.00560

Question:Converges from “above”? Contradiction to what we learnt about the nature of the FEA solution?

Reason:  This is an incompatible element ( See comments on p. 177).

Shells and Shell Elements

Shells – Thin structures witch span over curved surfaces.

Example:

Sea shell, egg shell (the wonder of the nature); Containers, pipes, tanks; Car bodies;

Roofs, buildings (the Superdome), etc. Forces in shells:

Membrane forces + Bending Moments

(cf.  plates:  bending only)

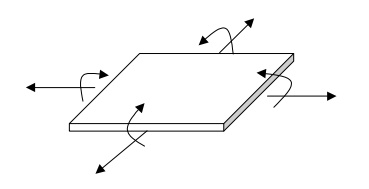
Example: A Cylindrical Container.

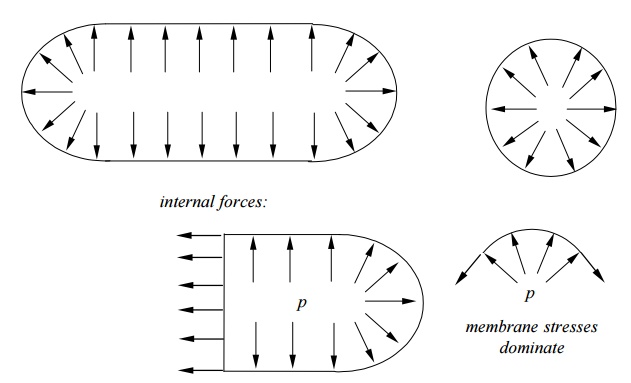
Shell Theory:

Thin shell theory

Shell theories are the most complicated ones to formulate and analyze in mechanics (Russian’s contributions).

Engineering Craftsmanship Demand strong analytical skill

Shell Elements:

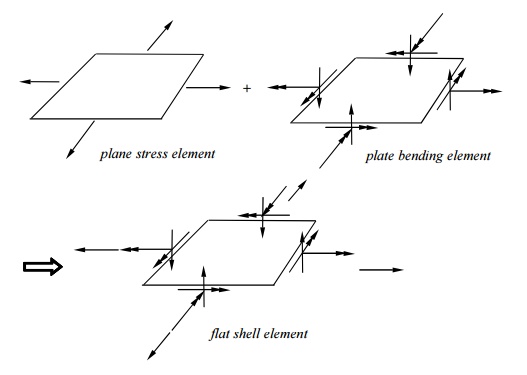
cf.: bar + simple beam element => general beam element.

DOF at each node:

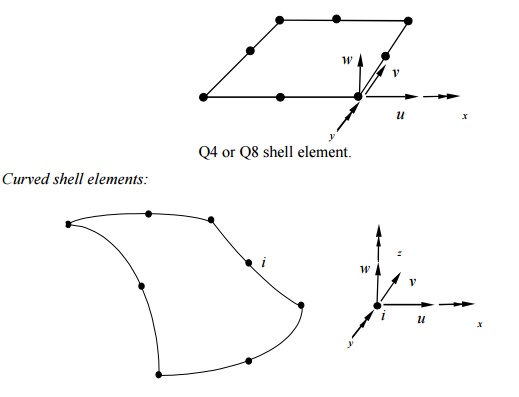
Based on shell theori es;

Most general shell el ements (flat shell and plate elements are subsets);

Complicated in form ulation.

Test Cases:

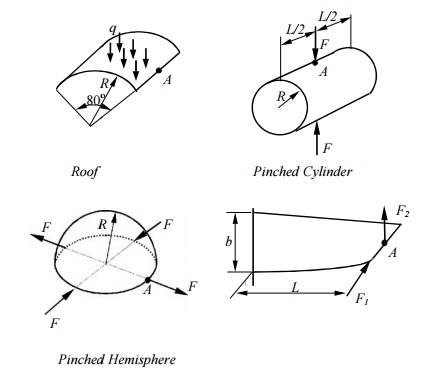
CONSISTENT MASS MAT RICES

Natural frequencies a nd modes

Frequency response ( F(t)=F_o sinwt) Transient

response (F(t) arbitrary)

1 Single DOF System

Free Vibration:

f(t) = 0 and no damping (c = 0) Eq. (1) becomes

mu ku

(meaning: inertia force + stiffness force = 0) Assume:

This is the circular natural frequency of the single DOF system (rad/s). The cyclic frequency (1/s = Hz) is

2.Multiple DOF System

Equation of Motion                         

Equation of motion for the whole structure is     

Mu    Cu   Ku       f (t) ,  (8)

in which:     u        nodal displacement vector,     

M      mass matrix,

C       damping matrix,

K stiffness matrix, f forcing vector.

Physical meaning of Eq. (8):

Inertia forces + Damping forces + Elastic forces

= Applied forces

Mass Matrices

Lumped mass matrix (1-D bar element):

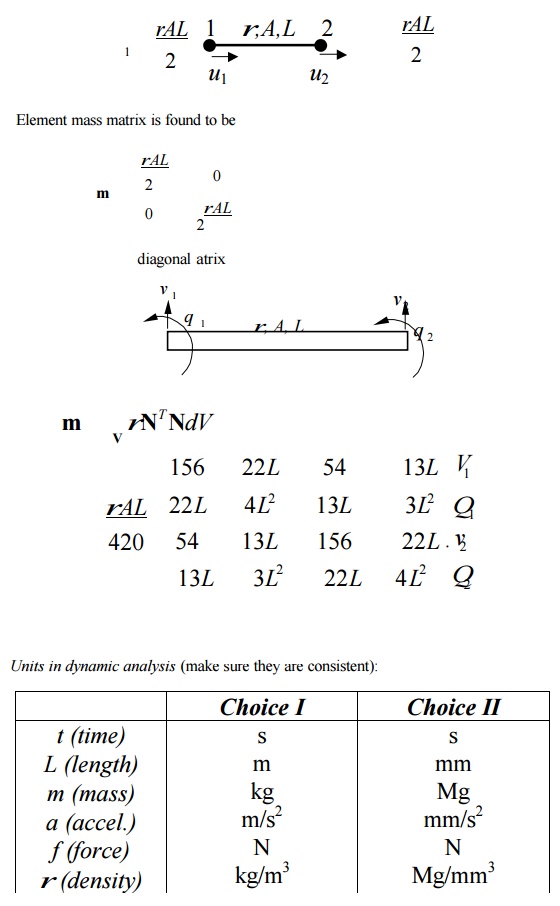
VECTOR ITERATION METHODS

Study of the dynamic characteristics of a structure: natural frequencies normal modes shapes)

Let f(t) = 0 and C = 0 (ignore damping) in the dynamic equation (8) and obtain

Mu Ku   0

Assume that displacements vary harmonically with time, that is,

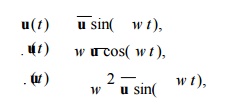
where  u  is the vector of nodal displacement amplitudes.

Eq. (12) yields,

This is a generalized eigenvalue problem (EVP).

Solutions?

This is an n-th order polynomial of from which we can find n solutions (roots) or eigenvalues

_i (i = 1, 2, …, n) are the natural frequencies (or characteristic frequencies) of the structure (the smallest one) is called the fundamental frequency. For each gives one

solution (or eigen) vector

if w_i  w_j . That is, modes are orthogonal (or independent) to each other with respect to K and

M matrices.

Note:

Magnitudes of displacements (modes) or stresses in normal mode analysis have no physical meaning.

For normal mode analysis, no support of the structure is necessary.

_i = 0  there are rigid body motions of the whole or a part of the structure. apply this to check

the FEA model (check for mechanism or free elements in the models).

Lower modes are more accurate than higher modes in the FE calculations (less spatial variations in the lower modes fewer elements/wave length are needed).

Example:

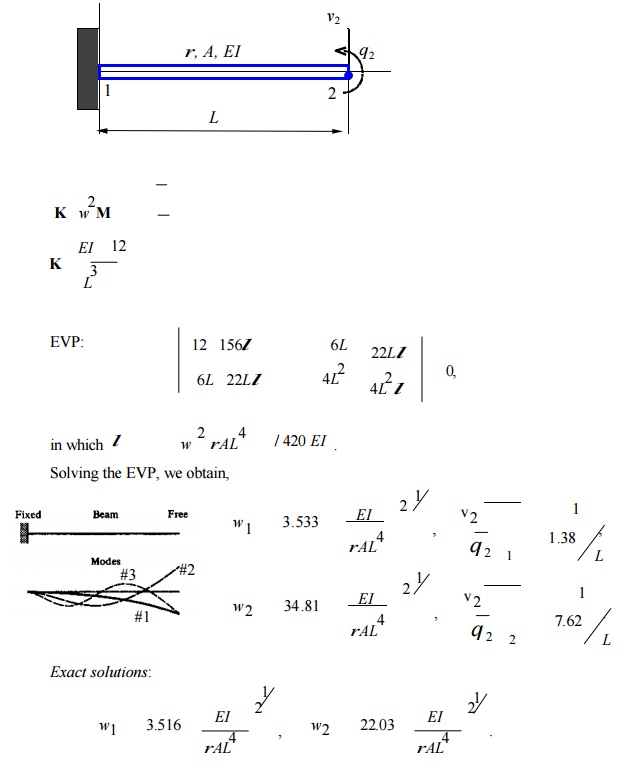
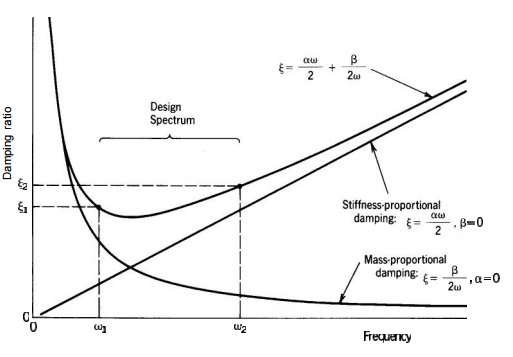
MODELLING OF DAMPING

Two commonly used models for viscous damping.

1 Proportional Damping (Rayleigh Damping)

C     M     K

(17)

where the constants   &   are found from

1,2 , 1 & 2 (damping ratio) being selected.

Modal Damping

Incorporate the viscous damping in modal equations.

Modal Equations

Use the normal modes (modal matrix) to transform the coupled system of dynamic equations to uncoupled system of equations.

We have

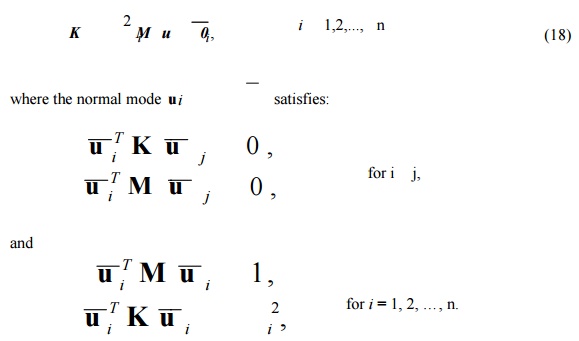
Equations in (22) or (24) are called modal equations. These are uncoupled, second-order differential equations, which are much easier to solve than the original dynamic equation (coupled system).

To recover u from z, apply transformation (21) again, once z is obtained from (24).

Notes:

Only the first few m odes may be needed in constructing the mod al matrix (i.e., could be an n m rectangular matrix with m<n). Thus, significant reduction in the

size of the system ca n be achieved.

Modal equations are best suited for problems in which higher mode s are not important (i.e., structural vibrations, but not shock loading).

2.Frequency Response Analysis

(Harmonic Response Analysis)

Ku    E u

Harmonicloading

(25)

Modal method:  Apply th e modal equations,

TRANSIENT RESPONSE ANALYSIS

(Dynamic Response/Time-History Analysis)

Structure response to arbitrary, time-dependent loading.

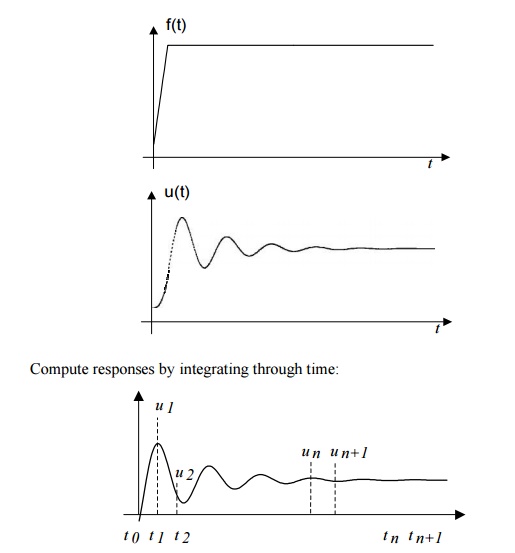
Compute responses by integrating through time:

B. Modal Method

First, do the transformation of the dynamic equations using the modal matrix before the time marching:

Then, solve the uncoupled equations using an integration method. Can use, e.g., 10%, of the total modes (m= n/10).

Uncoupled system, Fewer equations,

No inverse of matrices,

More efficient for large problems.

1Cautions in Dynamic Analysis

Symmetry: It should not be used in the dynamic analysis (normal modes, etc.) because symmetric structures can have antisymmetric modes.

Mechanism, rigid body motion means = 0. Can use this to check FEA models to see if they are properly connected and/or supported.

Input for FEA: loading F(t) or F( ) can be very complicated in real applications and often needs to be filtered first before used as input for FEA.

Examples

Impact, drop test, etc.

PROBLEM

In the spring structure shown k₁ = 10 lb./in., k₂ = 15 lb./in., k₃ = 20 lb./in., P= 5 lb. Determine the deflection at nodes 2 and 3.

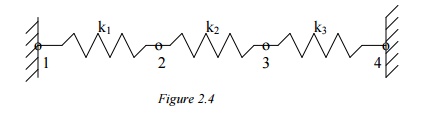
Solution:

Again apply the three steps outlined previously.

Step 1: Find the Element Stiffness Equations

Element 1:

Step 2: Find the Global stiffness matrix

Now the global structural equation can be written as above.

Step 3: Solve for Deflections

The known boundary conditions are: u₁ = u₄ = 0, F₃ = P = 3lb. Thus, rows and columns 1 and 4 will drop out, resulting in t following matrix equation,

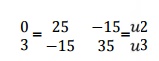
Solving, we get     u2 = 0.0692 & u3 = 0.1154    

PROBLEM                            

In the spring structure shown, k1 = 10 N/mm, k2 = 15 N/mm, k3 = 20 N/mm, k4 = 25 N/mm, k5 = 30 N/mm, k6 = 35 N/mm. F2 = 100 N. Find the deflections in all springs.

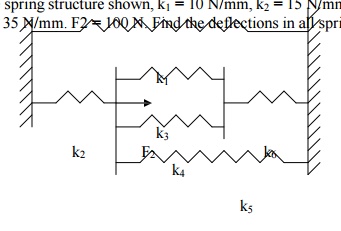
Solution:

Here again, we follow the three-step approach described earlier, without specifically mentioning at each step.

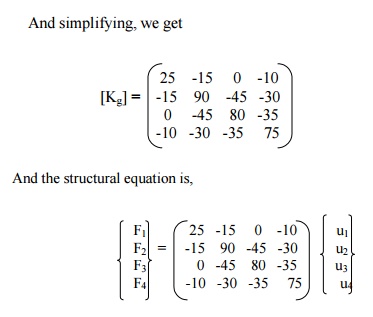
Now, apply the boundary conditions, u₁ = u₄ = 0, F₂ = 100 N. This is carried out by deleting the rows 1 and 4, columns 1 and 4, and replacing F₂ by 100N. The final matrix equation is,

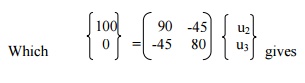
Deflections:                                                         

Spring 1:              u4 – u1       = 0                       

Spring 2:              u2 – u1       = 1.54590            

Spring 3:              u3 – u2       = -0.6763            

Spring 4:              u3      – u2   = -0.6763            

Spring 5:              u4      – u2   = -1.5459            

Spring 6:              u4      – u3   = -0.8696