Weak Formulati on of the Weighted Residual Statement

WEAK FORMULATI ON OF THE WEIGHTED RESIDUAL STATEMENT.

The analysis in Section as applied to the model problem provides an attra ctive perspective to the solution of certain partial differential equations: the solution is identified w ith a “point”, which minimizes an appropriately constructed functional over an admis- sible function space. Weak (variational) forms can be made fully equivalent to respective strong forms , as evidenced in the discussion of the weighted resid ual methods, under certain smoothness assumptions. However, the equivalence between weak (variati onal) forms and variational principles is not gu aranteed: indeed, there exists no general method of construct-

ing functionals I [u], whos e extremization recovers a desired weak (variational) form. In this

sense, only certain partial d ifferential equations are amenable to analysis and solution by variational methods.

Vainberg’s theorem provides the necessary and sufficient condition for the equivalence of a weak (variational) form to a functi onal extremization problem. If such equivalenc e holds, the functional is referred to as a potential.

Theorem (Vainberg)

Consider a weak (variational) form

G(u, δu) := B(u, δu) + (f, δu) + (q¯ , δu)Γq  = 0 ,

where u ∈ U , δu ∈ U0 , and f and q¯ are independent of u. Assume th at G pos- sesses a Gˆateaux derivative in a neighb orhood N of u, and the Gˆateaux differen- tial Dδu1 B(u, δu2) is

continuous  in u at every point  of N .

Then, the necessary and sufficient  condition for the above weak form to b e derivable from a

potential in N is that

Dδu1 G(u, δu2) = Dδu2 G(u, δu1) ,

Namely that Dδu1 G(u, δu2) be symmetric for all δu1, δu2 =  U0 and all u = N .

Preliminary to proving the above theorem, introduce the following two lemmas:

Lemma 1 Show that   Dv I[u]  =        lim

In the above derivation, no te that operations   and |ω=0 are not interchan geable (as they

both refer to the same variable ω), while lim∆ω→0 and |ω=0 are interchangeable, conditional upon sufficient smoothness of I [u].

Lemma 2 (Lagrange’s formula)

Let I [u] be a functional with Gateaux derivatives everywhere, and u, u + δu be any points of U. Then,

I [u + δu] − I [u ] = Dδu I [u + ǫ δu]      0 < ǫ < 1.

To prove Lemma 2, fix u and u + δu in U, and define function f on R as

f(ω)  :=  I[u +  ω δu] .

It follows that

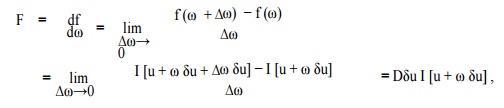
Where Lemma 1 was inv oked. Then, u s i n g the standard mean-value theorem of calculus,