Principle Of Stationery Total Potential (PSTP)

PRINCIPLE OF STATIONERY TOTAL POTENTIAL (PSTP)

1 Potential energy in elastic bodies

Potential energy is the capacity to do the work by the force acting on deformable bodies; the forces acting on a body may be classified as external forces and internal forces. External forces are the applied loads while internal force is the stresses developed in the body. Hence the total potential energy is the sum of internal and external potential energy.

Consider a spring mass system let its stiffness be k and length L, due to a force P let it extend

by u

The load P moves down by distance u. hence it loses its capacity to do work by P u. the external potential energy in this case is given by.

H = -P u

Average force = Ku/2

The energy stored in the spring due to strain = Average force x Deflection

= Ku/2 x u

Total potential energy in the spring  =  K u2- P u

2 Principle of Minimum Potential Energy

From the expression for total potential energy

Hence we can conclude that a deformable body is in equilibrium when the potential energy is having stationary value.

Hence the principle of minimum potential energy states among all the displacement equations that internal compatibility and the boundary condition those that also satisfy the equation of equilibrium make the potential energy a minimum is a stable system

Problem 7

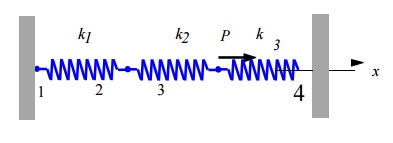
Given:         For the spring system shown above,

k1      100 N / mm,

k2      200 N / mm,

k3      100 N / mm

P       500 N,

u1      0

u4      0

Find: (a) The global stiffness matrix

(b)     Displacements of nodes 2 and 3

(c)      The reaction forces at nodes 1 and 4

(d)     the force in the spring 2

Solution:

(a)  The element stiffness matrices are

Problem 8

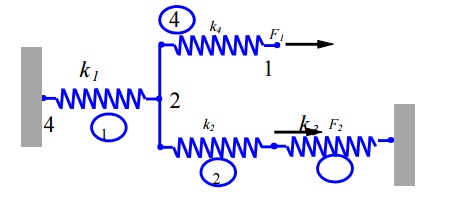
For the spring system with arbitrarily numbered nodes and elements, as shown above, find the global stiffness matrix.

Solution:

First we construct the following

Element Connectivity Table

Element      : Node i (1) : Node j (2)

1        4        2

2        2        3

3        3        5

4        2        1

Which specifies the global node numbers corresponding to the local node numbers for each element? Then we can write the element stiffness matrices as follows

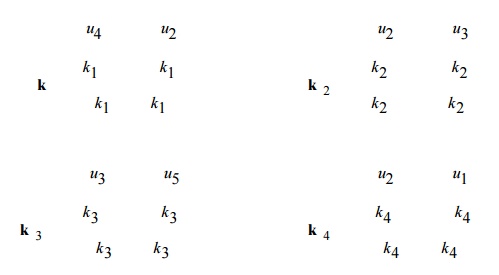
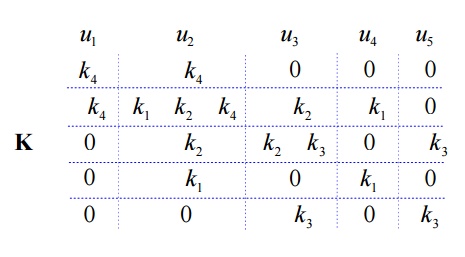
Finally, applying the superposition method, we obtain the global stiffness matrix as follows

We may note that N1 and N2 obey the definition of shape function that is the shape function will have a value equal to unity at the node to which it belong and zero value at other  nodes.