Types of Stresses

TYPES OF STRESSES :

Only two basic stresses exists : (1) normal stress and (2) shear shear stress. Other stresses either are similar to these basic stresses or are a combination of these e.g. bending stress is a combination tensile, compressive and shear stresses. Torsional stress, as encountered in twisting of a shaft is a shearing stress.

Let us define the normal stresses and shear stresses in the following sections.

Normal stresses : We have defined stress as force per unit area. If the stresses are normal to the areas concerned, then these are termed as normal stresses. The normal stresses are generally denoted by a Greek letter ( s )

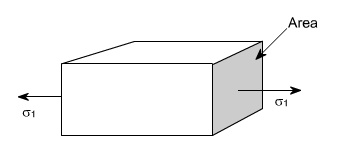
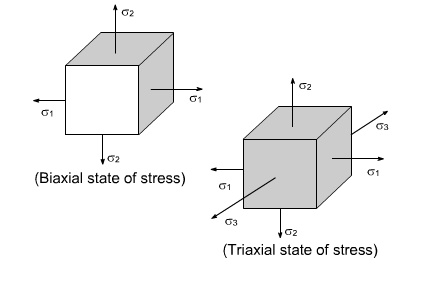
This is also known as uniaxial state of stress, because the stresses acts only in one direction however, such a state rarely exists, therefore we have biaxial and triaxial state of stresses where either the two mutually perpendicular normal stresses acts or three mutually perpendicular normal stresses acts as shown in the figures below :

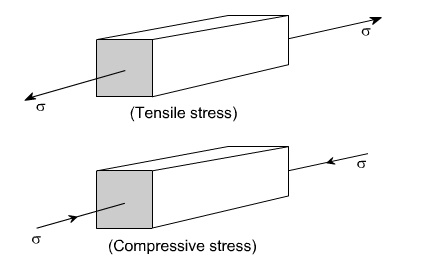
Tensile or compressive stresses :

The normal stresses can be either tensile or compressive whether the stresses acts out of the area or into the area

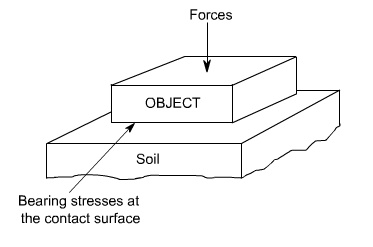
Bearing Stress : When one object presses against another, it is referred to a bearing stress ( They are in fact the compressive stresses ).

Shear stresses :

Let us consider now the situation, where the cross –sectional area of a block of material is subject to a distribution of forces which are parallel, rather than normal, to the area concerned. Such forces are associated with a shearing of the material, and are referred to as shear forces. The resulting force interistes are known as shear stresses.

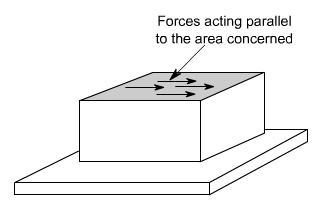
The resulting force intensities are known as shear stresses, the mean shear stress being equal to

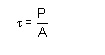
Where P is the total force and A the area over which it acts.

Stress is defined as the force per unit area. Thus, the formula for calculating stress is:

s= F/A

Where s denotes stress, F is load and A is the cross sectional area. The most commonly used units for stress are the SI units, or Pascals (or N/m²), although other units like psi (pounds per square inch) are sometimes used.

Forces may be applied in different directions such as:

•                  Tensile or stretching

•                  Compressive or squashing/crushing

•                  Shear or tearing/cutting

•                  Torsional or twisting

This gives rise to numerous corresponding types of stresses and hence measure/quoted strengths. While data sheets often quote values for strength (e.g compressive strength), these values are purely uniaxial, and it should be noted that in real life several different stresses may be acting.

Tensile Strength

The tensile strength is defined as the maximum tensile load a body can withstand before failure divided by its cross sectional area. This property is also sometimes referred to Ultimate Tensile Stress or UTS.

Typically, ceramics perform poorly in tension, while metals are quite good. Fibres such as glass, Kevlar and carbon fibre are often added polymeric materials in the direction of the tensile force to reinforce or improve their tensile strength.

Compressive Strength

Compressive strength is defined as the maximum compressive load a body can bear prior to failure, divided by its cross sectional area.

Ceramics typically have good tensile strengths and are used under compression e.g. concrete.

Shear Strength

Shear strength is the maximum shear load a body can withstand before failure occurs divided by its cross sectional area.

This property is relevant to adhesives and fasteners as well as in operations like the guillotining of sheet metals.

Torsional Strength

Torsional strength is the maximum amount of torsional stress a body can withstand before it fails, divided by its cross sectional area.

This property is relevant for components such as shafts.

Yield Strength

Yield strength is defined as the stress at which a material changes from elastic deformation to plastic deformation. Once the this point, known as the yield point is exceeded, the materials will no longer return to its original dimensions after the removal of the stress.

Stress is defined as the force per unit area. Thus, the formula for calculating stress is:

Where s denotes stress, F is load and A is the cross sectional area. The most commonly used units for stress are the SI units, or Pascals (or N/m²), although other units like psi (pounds per square inch) are sometimes used.

Forces may be applied in different directions such as:

•                  Tensile or stretching

•                  Compressive or squashing/crushing

•                  Shear or tearing/cutting

•                  Torsion or twisting

This gives rise to numerous corresponding types of stresses and hence measure/quoted strengths. While data sheets often quote values for strength (e.g compressive strength), these values are purely uni axial, and it should be noted that in real life several different stresses may be acting

Deformation of simple bars under axial load Deformation of bodies

Concept of strain : if a bar is subjected to a direct load, and hence a stress the bar will change in length. If the bar has an original length L and changes by an amount dL, the strain produce is defined as follows:

Strain is thus, a measure of the deformation of the material and is a non dimensional Quantity i.e. it has no units. It is simply a ratio of two quantities with the same unit.

Shear strain: As we know that the shear stresses acts along the surface. The action of the stresses is to produce or being about the deformation in the body consider the distortion produced b shear sheer stress on an element or rectangular block This shear strain or slide is f and can be defined as the change in right angle. or The angle of deformation g is then termed as the shear strain. Shear strain is measured in radians & hence is non –dimensional

i.e. it has no unit .So we have two types of strain i.e. normal stress & shear stresses.

Hook's Law :

A material is said to be elastic if it returns to its original, unloaded dimensions when load is removed.

Hook's law therefore states that Stress ( s ) a strain( Î )

Modulus of elasticity : Within the elastic limits of materials i.e. within the limits in which Hook's law applies, it has been shown that

Stress / strain = constant

This constant is given by the symbol E and is termed as the modulus of elasticity or Young's modulus of elasticity Thus ,The value of Young's modulus E is generally assumed to be the same in tension or compression and for most engineering material has high, numerical value of the order of 200 GPa

Poisson's ratio: If a bar is subjected to a longitudinal stress there will be a strain in this direction equal to s / E . There will also be a strain in all directions at right angles to s . The final shape being shown by the dotted lines.

It has been observed that for an elastic materials, the lateral strain is proportional to the longitudinal strain. The ratio of the lateral strain to longitudinal strain is known as the poison's ratio .

Poison's ratio ( m ) = - lateral strain / longitudinal strain

For most engineering materials the value of m his between 0.25 and 0.33.

Deformation of compound bars under axial load

For a prismatic bar loaded in tension by an axial force P, the elongation of the bar can be determined as Suppose the bar is loaded at one or more intermediate positions, then equation

(1) can be readily adapted to handle this situation, i.e. we can determine the axial force in each part of the bar i.e. parts AB, BC, CD, and calculate the elongation or shortening of each part separately, finally, these changes in lengths can be added algebraically to obtain the total charge in length of the entire bar.

When either the axial force or the cross –sectional area varies continuosly along the axis of the bar, then equation (1) is no longer suitable. Instead, the elongation can be found by considering a deferential element of a bar and then the equation (1) becomes i.e. the axial force Pxand area of the cross –section Ax must be expressed as functions of x. If the expressions for Pxand Ax are not too complicated, the integral can be evaluated analytically,

otherwise Numerical methods or techniques can be used to evaluate these integrals.