Chapter: Mechanical : Strength of Materials : Stress, Strain and Deformation of Solids
Elastic constants
Elastic constants
Relation between E, G and u :
Let us establish a relation among the elastic constants E,G and u. Consider a cube of material of side „a' subjected to the shown in the figure and producing the strained shape as shown in the figure below.
Assuming that the strains are small and the angle A C B may be taken as 450.
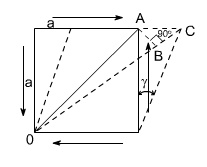
Therefore strain on the diagonal OA
= Change in length / original length
Since angle between OA and OB is very small hence OA @ OB therefore BC, is the change in the length of the diagonal OA

Now this shear stress system is equivalent or can be replaced by a system of direct stresses at 450 as shown below. One set will be compressive, the other tensile, and both will be equal in value to the applied shear strain.

Thus, for the direct state of stress system which applies along the diagonals:
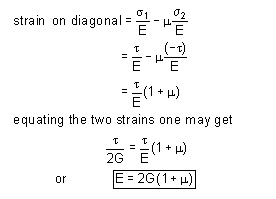
We have introduced a total of four elastic constants, i.e E, G, K and g. It turns out that not all of these are independent of the others. Infact given any two of then, the other two can be found.
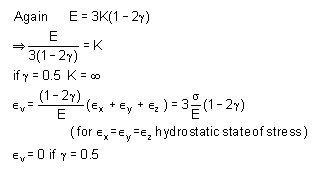
irrespective of the stresses i.e, the material is incompressible.
When g = 0.5 Value of k is infinite, rather than a zero value of E and volumetric strain is zero, or in other words, the material is incompressible.
Relation between E, K and u :
Consider a cube subjected to three equal stresses s as shown in the figure below
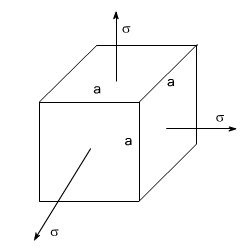
The total strain in one direction or along one edge due to the application of hydrostatic stress or volumetric stress s is given as

Relation between E, G and K :
The relationship between E, G and K can be easily determained by eliminating u from the already derived relations
E = 2 G ( 1 + u ) and E = 3 K ( 1 - u )
Thus, the following relationship may be obtained
Relation between E, K and g :
From the already derived relations, E can be eliminated
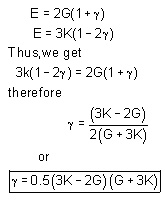
Engineering Brief about the elastic constants :
We have introduced a total of four elastic constants i.e E, G, K and u. It may be seen that not all of these are independent of the others. Infact given any two of them, the other two can be determined. Further, it may be noted that
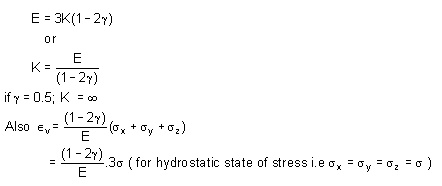
hence if u = 0.5, the value of K becomes infinite, rather than a zero value of E and the volumetric strain is zero or in other words, the material becomes incompressible
Further, it may be noted that under condition of simple tension and simple shear, all real materials tend to experience displacements in the directions of the applied forces and Under hydrostatic loading they tend to increase in volume. In other words the value of the elastic constants E, G and K cannot be negative
Therefore, the relations
E = 2 G ( 1 + u )
E = 3 K ( 1 - u )
Yields
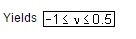
In actual practice no real material has value of Poisson's ratio negative . Thus, the value of u cannot be greater than 0.5, if however u > 0.5 than Îv = -ve, which is physically unlikely because when the material is stretched its volume would always increase.
Elastic constant - problems
1. The Young’s modulus and the Shear respectively. What is its Bulk modulus?
2. A 20 mm diameter bar was subjected to an axial pull of 40 KN and change in diameter was found to be 0.003822 mm. Find th modulus if the shear modulus of material of the bar is 76.923 GPa.
3. A steel plate 300 mm long, 60 mm wide and 30 mm deep is acted upon by the forces
shown in Fig. Determine the change in volume Take E = 200 KN/mm2 and Poiss 0.3.
4. A bar of 30 mm x 30 mm x 250 mm long was subjected to a pull of 90 KN in the direction of its length. Then extension of the bar was found to be 0.125 mm, while the decrease in each lateral dimension was found toPisb ratio and rigidity modulus of the bar.
Related Topics