Types of Distribution - Biostatistics

Types of Distribution:

     Though this universe is full of uncertainty and variability, a large set of experimental/biological observations always tend towards a normal distribution. This unique behavior of data is the key to entire inferential statistics. There are two types of distribution.

Gaussian /normal distribution: If data is symmetricallydistributed on both sides of mean and form a bell-shaped curve in frequency distribution plot, the distribution of data is called normal or Gaussian. The noted statistician professor Gauss developed this, and therefore, it was named after him. The normal curve describes the ideal distribution of continuous values i.e. heart rate, blood sugar level and Hb % level. Whether our data is normally distributed or not, can be checked by putting our raw data of study directly into computer software and applying distribution test. 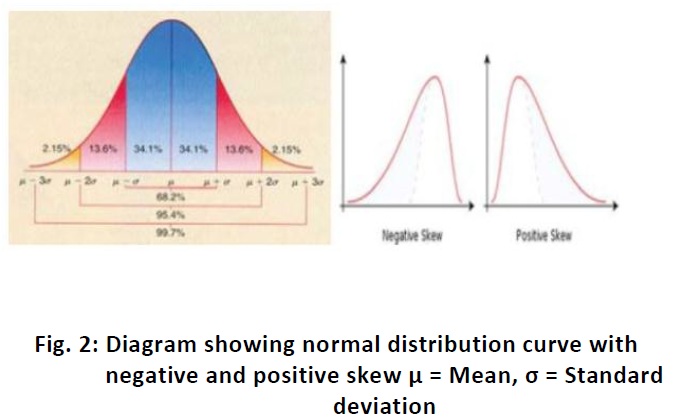Statistical treatment of data can generate a number of useful measurements, the most important of which are mean and standard deviation of mean. In an ideal Gaussian distribution, the values lying between the points 1 SD below and 1 SD above the mean value (i.e. ± 1 SD) will include 68.27% of all values. The range, mean ± 2 SD includes approximately 95% of values distributed about this mean, excluding 2.5% above and 2.5% below the range [Fig. 2]. In ideal distribution of thevalues: the mean, mode, and median are equal withinpopulation under study. Even if distribution in original population is far from normal, the distribution of sample averages tend to become normal as size of sample increases. This is the single most important reason for the curve of normal distribution. Various methods of analysis are available to make assumptions about normality, including‘t’ test and analysis of variance (ANOVA). In normal distribution, skew is zero. If the difference (mean–median) is positive, the curve is positively skewed and if it is (mean–median) negative, the curve is negatively skewed, and therefore, measure of central tendency differs [Fig. 2].

 Non-Gaussian (non-normal) distribution: If the data is skewedon one side, then the distribution is non-normal. It may be binominal distribution or Poisson distribution. In binominal distribution, event can have only one of two possible outcomes such as yes/no, positive/negative, survival/death, and smokers/non-smokers. When distribution of data is non-Gaussian, different test like Wilcoxon, Mann-Whitney, Kruskal-Wallis, and Friedman test can be applied depending on nature of data.

Standard Error of Mean

Since we study some points or events (sample) to draw conclusions about all patients or population and use the samplemean (M) as an estimate of the population mean (M1), we need to know how far M can vary from M1 if repeated samples of size N are taken. A measure of this variability is provided by Standard error of mean (SEM), which is calculated as (SEM = SD/√n). SEM is always less than SD. What SD is to the sample, the SEM is to the population mean.