Geometry | Term 2 Chapter 4 | 6th Maths - Types and Properties of Triangles | 6th Maths : Term 2 Unit 4 : Geometry
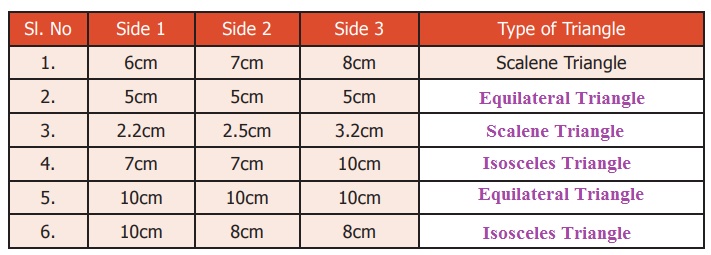
Chapter: 6th Maths : Term 2 Unit 4 : Geometry
Types and Properties of Triangles
Types
and Properties of Triangles
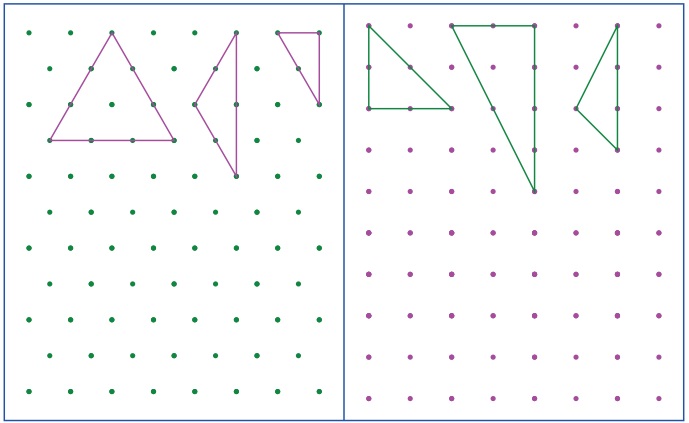
Some triangles are drawn in the dotted sheet. Try
to draw as many triangles as you can. Then, measure the sides and angles
of all triangles and fill the table given below
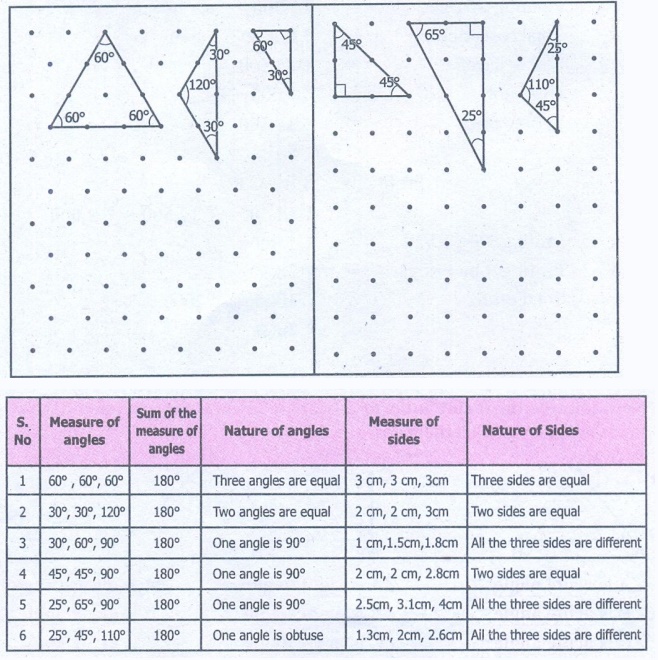
From the table, we observe the following:
In a triangle,
* If the measure of all angles are different, then
all sides are different.
* If the measure of two angles are equal, then two
sides are equal.
* If the measure of three angles are equal, then
three sides are equal and each angle measures 60°
Sum of three angles of a triangle is 180° .
Activity
Students are divided into groups and
each group is given 3 sticks of length 9 units, 2 sticks of length 3 units, 2 sticks
of length 2 units, 1 stick of length 5 units and 1 stick of length 4 units. Using
the given sticks they are asked to form three triangles, find the length of the
sides of each triangle and tabulate them.

Read the table and answer the following
questions.
1. Was each group able to form 3 triangles?
2. In each of the triangle formed,
how many sides are equal?
1.
Types of triangle based on its sides
i) If three sides of a triangle are different in
lengths, then it is called a Scalene Triangle
Examples:
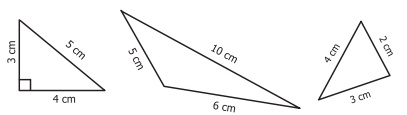
ii) If any two sides of a triangle are equal in
length, then it is called an Isosceles Triangle
Examples:

iii) If three sides of a triangle are equal in length,
then it is called an Equilateral Triangle
Examples:
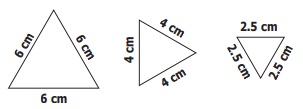
Thus, based on the sides of triangles,
we can classify triangles into 3 types.
Try these
Complete the following table. In any
triangle,
2.
Types of triangle based on its angles
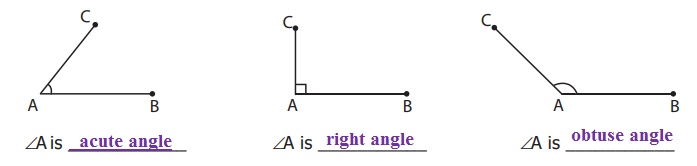
Write the given angles as acute, obtuse or right
angle formed by two line segments AB and AC
Now, join the third side to form a triangle in each
case and identify the kinds of angles and list them down.

∠A is acute angle
∠B is acute angle
∠C is acute angle
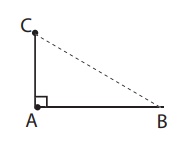
∠A is right angle
∠B is acute angle
∠C is acute angle

∠A is obtuse angle
∠B is acute angle
∠C is acute angle
Now carefully look at these three triangles,
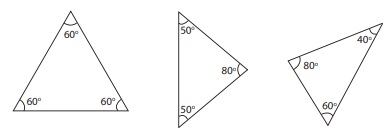
(i) If three angles
of a triangle are acute angles (between 0° and 90°), then it is called an Acute Angled Triangle.
Examples:
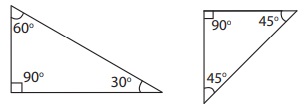
ii) If an angle of a triangle is a right angle (90°),
then it is called a Right Angled Triangle.
Examples:
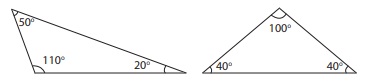
iii) If an angle of a triangle is an obtuse angle
(between 90° and 180° ), then it is called an Obtuse
Angled Triangle.
Examples:
Thus, based on the angles of triangles,
we can classify triangles into 3 types.
Try these
Complete the table

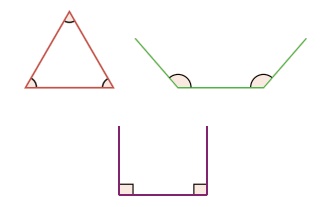
DO YOU KNOW
A triangle can have three acute angles,
but cannot have more than one right angle or an obtuse angle.
Activity
In the given figure, there are some
triangles. Measure their sides and angles and name them in two ways. (One is done
for you )
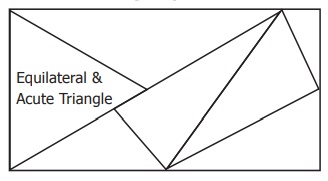
3.
Triangle Inequality property
Think about the situation:
Three students Kamala, Madhan and Sumathi are asked
to form triangles with the given sticks of measure 6cm,
8cm, 5cm; 4cm, 10cm, 5cm and 10cm, 6cm, 4cm respectively. All of them try to form
a triangle. While Kamala, the first girl is successful in forming a triangle, Madhan
and Sumathi, next to Kamala are struggling. Why?

When they are trying to join the ends of the two
smaller sticks, they find that the two smaller sticks coincide with the longer stick
or shorter than the longer stick and they are unable to form triangles. From this,
they understand that,
To form a triangle the sum of two smaller sides
must be greater than the third side. Thus,
In a triangle, the sum of any two
sides of a triangle
is greater than the third side.
This is known as Triangle Inequality
property.
AB + BC > CA
BC + CA > AB
CA + AB > BC
Note
If three sides are equal in length, then definitely a triangle can be formed
DO YOU KNOW
If two sides of the triangle are given, then the length of the third side will
lie between the difference and sum of the lengths of two given sides.
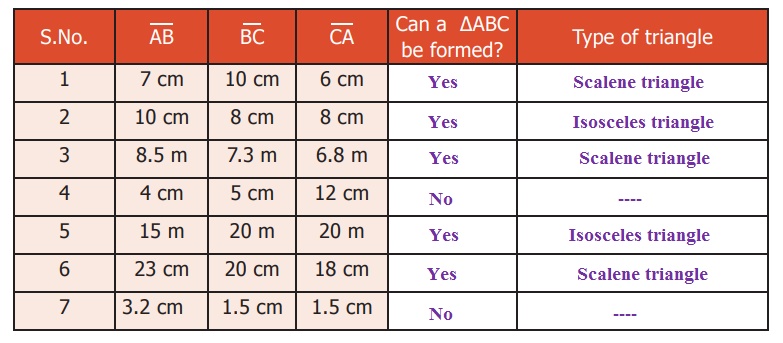
Example 1:
Can a triangle be formed with 7 cm, 10 cm and 5 cm as its sides
Solution: Instead of checking triangle inequality by all the
sides in the triangle, check only with two smaller sides.
Sum of two smaller sides
of the triangle = 5+7=12 cm > 10 cm, the third side.
It is greater than the third side.
So, a triangle can be formed with the given sides.
Example 2:
Can a triangle be formed with 7 cm, 7 cm and 7 cm as its sides?
Solution:
If three sides are equal, then definitely a triangle
can be formed, as the triangle inequality is satisfied.
Example 3:
Can a triangle be formed with 8 cm, 3 cm and 4 cm as its sides?
Solution:
The sum of two smaller sides = 3+4=7 cm < 8 cm, the third side.
It is less than the third side.
So, a triangle cannot be formed with the given sides.
Try these
Can a triangle be formed with the
given sides? If yes, state the type of triangle formed.
Example 4:
Can a triangle be formed with the angles 80°, 30°
, 40°?
Solution:
The sum of three angles = 80° + 30° + 40° = 150°
(not equal to 180° )
In a triangle, the sum of three angles is 180°.
So, a triangle cannot be formed with the given angles.
Think
Can the difference between two larger sides be less than the third side?
Activity
A triangle game: In each turn a student
must draw one line connecting two dots. A line should not cross other lines or touch
other dots than the two that are connected to. If a student closes a triangle with
his line then he gets a point. Once there are no more lines that can be drawn the
game is over and the student who gains more points wins the game.
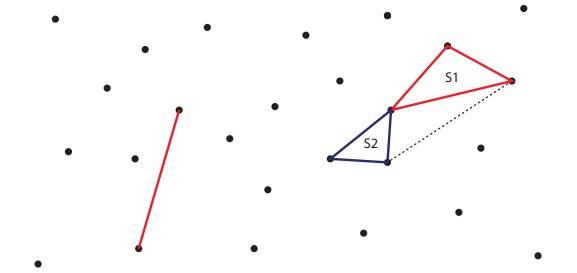
Think
In a right triangle, what measures
can the other two angles have?
Related Topics