Traveling Salesman Problem

TRAVELING SALESMAN PROBLEM

We will be able to apply the dynamic programming technique to instances of the traveling salesman problem, if we come up with a reasonable lower bound on tour lengths.

One very simple lower bound can be obtained by finding the smallest element in the intercity distance matrix D and multiplying it by the number of cities it. But there is a less obvious and more informative lower bound, which does not require a lot of work to compute.

It is not difficult to show that we can compute a lower bound on the length I of any tour as follows.

For each city i, 1 ≤ i ≤ n, find the sum si of the distances from city i to the two nearest cities; compute the sums of these n numbers; divide the result by 2, and, it all the distances are integers, round up the result to the nearest integer:

lb=|S/2|

b) State-space tree of the branch-and- bound algorithm applied to this graph.

(The list of vertices in a node specifies a beginning part of the Hamiltonian circuits represented by the node.)

For example, for the instance of the above figure, formula yields

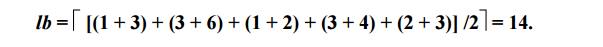
We now apply the branch and bound algorithm, with the bounding function given by formula, to find the shortest Hamiltonian circuit for the graph of the above figure (a). To reduce the amount of potential work, we take advantage of two observations.

First, without loss of generality, we can consider only tours that start at a.

Second, because our graph is undirected, we can generate only tours in which b is visited before c. In addition, after visiting n-1 = 4 cities, a tour has no choice but to visit the remaining unvisited city and return to the starting one. The state-space tree tracing the algorithm‘s application is given in the above figure (b).

The comments we made at the end of the preceding section about the strengths and weaknesses of backtracking are applicable to branch-and-bound as well. To reiterate the main point: these state-space tree techniques enable us to solve many large instances of difficult combinatorial problems.

As a rule, however, it is virtually impossible to predict which instances will be solvable in a realistic amount of time and which will not.

Incorporation of additional information, such as symmetry of a game‘s board, can widen the range of solvable instances. Along this line, a branch-and- bound algorithm can be sometimes accelerated by knowledge of the objective function‘s value of some nontrivial feasible solution.

The information might be obtainable—say, by exploiting specifics of the data or even, for some problems, generated randomly—before we start developing a state-space tree. Then we can use such a solution immediately as the best one seen so far rather than waiting for the branch-and-bound processing to lead us to the first feasible solution.

In contrast to backtracking, solving a problem by branch-and-bound ha both the challenge and opportunity of choosing an order of node generation and finding a good bounding function.

Though the best-first rule we used above is a sensible approach, it mayor may not lead to a solution faster than other strategies.