Chapter: Analysis and Design of Algorithm : Backtracking
Backtracking Algorithms
BACKTRACKING
Many
problems are difficult to solve algorithmically. Backtracking makes it possible
to solve at least some large instances of difficult combinatorial problems.
GENERAL METHOD
The
principal idea is to construct solutions one component at a time and evaluate
such partially constructed candidates as follows.
If a
partially constructed solution can be developed further without violating the
problem‘s
constraints, it is done by taking the first remaining legitimate option for the
next component.
If there
is no legitimate option for the next component, no alternatives for any
remaining
component need to be considered. In this case, the algorithm backtracks to
replace the last component of the partially constructed solution with its next
option.
STATE-SPACE TREE
It is
convenient to implement this kind of processing by constructing a tree of
choices being made, called the state-space
tree. Its root represents an initial state before the search for a solution
begins. The nodes of the first level in the tree represent the choices made for
the first component of a solution; the nodes of the second level represent the
choices for the second component, and so on.
A node in
a state-space tree is said to be promising
if it corresponds to a partially constructed solution that may still lead to a
complete solution; otherwise, it is called nonpromising.
Leaves
represent either nonpromising dead ends
or complete solutions found by the
algorithm.
N-QUEENS PROBLEM
The
problem is to place it queens on an n-by-n chessboard so that no two queens
attack each other by being in the same row or in the same column or on the same
diagonal. For n = 1, the problem has a trivial solution, and it is easy to see
that there is no solution for n = 2 and n =3. So let us consider the
four-queens problem and solve it by the backtracking technique. Since each of
the four queens has to be placed in its own row, all we need to do is to assign
a column for each queen on the board presented in the following figure.
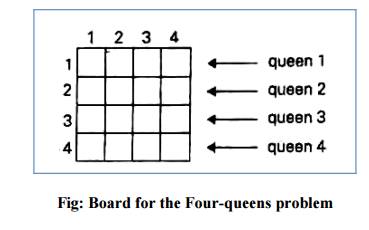
Steps to be followed
We start with the empty board and then place queen 1 in the first possible position of its row, which is in column 1 of row 1.
Then we place queen 2, after trying unsuccessfully columns 1 and 2, in the first acceptable position for it, which is square (2,3), the square in row 2 and column 3. This proves to be a dead end because there i no acceptable position for queen 3. So, the algorithm backtracks and puts queen 2 in the next possible position at (2,4).
Then queen 3 is placed at (3,2), which proves to be another dead end.
The algorithm then backtracks all the way to queen 1 and moves it to (1,2). Queen 2 then goes to (2,4), queen 3 to (3,1), and queen 4 to (4,3), which is a solution to the problem.
(x denotes an unsuccessful attempt to place a queen in the indicated column. The numbers above the nodes indicate the order in which the nodes are generated)
If other solutions need to be found, the algorithm can simply resume its operations at the leaf at which it stopped. Alternatively, we can use the board‘s symmetry for this purpose.
SUBSET-SUM PROBLEM
Subset-Sum Problem is
finding a subset of a given set S = {s1,s2….sn}
of n positive integers whose sum is equal to a given positive
integer d.
For
example, for S = {1, 2, 5, 6, 8) and d = 9, there are two solutions: {1, 2, 6}
and {1, 8}. Of course, some instances of this problem may have no solutions.
that s1
≤ s2
≤ ……. ≤ sn
The
state-space tree can be constructed as a binary tree as that in the following
figure for the instances S = (3, 5, 6, 7) and d = 15.
The root
of the tree represents the starting point, with no decisions about the given
elements made as yet.
Its left
and right children represent, respectively, inclusion and exclusion ofs1 in a
set being sought.
Similarly,
going to the left from a node of the first level corresponds to inclusion of
s2, while going to the right corresponds to its exclusion, and soon.
Thus, a
path from the root to a node on the ith level of the tree indicates which of
the first i numbers have been included in the subsets represented by that node.
We record
the value of s‘ the sum of these numbers, in the node, Ifs is equal to d. we
have a solution to the problem.
We can
either, report this result and stop or, if all the solutions need to he found,
continue by backtracking to the node‘s parent.
If s‘ is
not equal to d, we can terminate the node as nonpromising if either of the two
inequalities holds:

1. Pseudocode For Backtrack
Algorithms

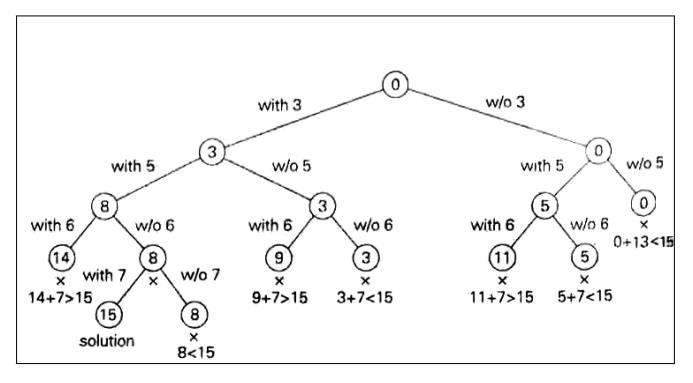
Fig: Complete state-space tree of
the backtracking algorithm
(applied
to the instance S = (3, 5, 6, 7) and d = 15 of the subset-sum problem. The
number inside a node is the sum of
the elements already included in subsets represented by the node. The
inequality below a leaf indicates the reason for its termination)
GRAPH COLORING
A
coloring of a graph is an assignment of a color to each vertex of the graph so
that no two vertices connected by an edge have the same color. It is not hard
to see that our problem is one of coloring the graph of incompatible turns
using as few colors as possible.
The
problem of coloring graphs has been studied for many decades, and the theory of
algorithms tells us a lot about this problem. Unfortunately, coloring an
arbitrary graph with as few colors as possible is one of a large class of
problems called "NP-complete problems," for which all known solutions
are essentially of the type "try all possibilities."
A
k-coloring of an undirected graph G = (V, E) is a function c : V → {1, 2,...,
k} such that c(u) ≠ c(v) for every edge (u, v) E. In other words, the numbers
1, 2,..., k represent the k colors, and adjacent vertices must have different
colors. The graph-coloring problem is to determine the minimum number of colors
needed to color a given graph.
a. Give an efficient algorithm to determine a 2-coloring of a graph if one exists.
b.
Cast the graph-coloring problem as a decision
problem. Show that your decision problem is solvable in polynomial time if and
only if the graph-coloring problem is solvable in polynomial time.
c.
Let the language 3-COLOR be the set of graphs that
can be 3-colored. Show that if 3-COLOR is NP-complete, then your decision
problem from part (b) is NP-complete.
To prove
that 3-COLOR is NP-complete, we use a reduction from 3-CNF-SAT. Given a formula
φ of m clauses on n variables x, x,..., x, we construct a graph G = (V, E) as
follows.
The set V
consists of a vertex for each variable, a vertex for the negation of each
variable, 5 vertices for each clause, and 3 special vertices: TRUE, FALSE, and
RED. The edges of the graph are of two types: "literal" edges that
are independent of the clauses and "clause" edges that depend on the
clauses. The literal edges form a triangle on the special vertices and also
form a triangle on x, ¬x, and RED for i = 1, 2,..., n.
d.
Argue that in any 3-coloring c of a graph
containing the literal edges, exactly one of a variable and its negation is
colored c(TRUE) and the other is colored c(FALSE).
Argue
that for any truth assignment for φ, there is a 3-coloring of the graph
containing just the literal edges.
The
widget is used to enforce the condition corresponding to a clause (x y z). Each
clause requires a unique copy of the 5 vertices that are heavily shaded; they
connect as shown to the literals of the clause and the special vertex TRUE.
e.
Argue that if each of x, y, and z is colored
c(TRUE) or c(FALSE), then the widget is 3-colorable if and only if at least one
of x, y, or z is colored c(TRUE).
f.
Complete the proof that 3-COLOR is NP-complete.
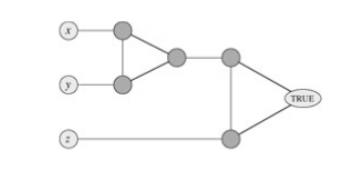
Fig: The
widget corresponding to a clause (x y
z), used in Problem
HAMILTONIAN CIRCUIT PROBLEM
As our
next example, let us consider the problem of finding a Hamiltonian circuit in
the graph of Figure 11.3a. Without loss of generality, we can assume that if a
Hamiltonian circuit exists, it starts at vertex a. Accordingly, we make vertex
a the root of the state-space tree (Figure 11.3b).
The first
component of our future solution, if it exists, is a first intermediate vertex
of a Hamiltonian cycle to be constructed. Using the alphabet order to break the
three-way tie among the vertices adjacent to a, we select vertex b. From b, the
algorithm proceeds to c, then to d, then to e, and finally to f, which proves
to be a dead end. So the algorithm backtracks from f to e, then to d. and then
to c, which provides the first alternative for the algorithm to pursue.
Going
from c to e eventually proves useless, and the algorithm has to backtrack from
e to c and then to b. From there, it goes to the vertices f, e, c, and d, from
which it can legitimately return to a, yielding the Hamiltonian circuit a, b,
f, e, c, d, a. If we wanted to find another Hamiltonian circuit, we could
continue this process by backtracking from the leaf of the solution found.
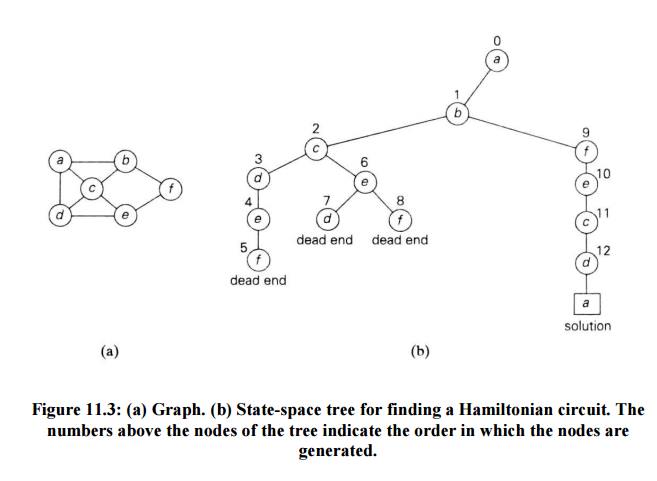
Figure 11.3: (a) Graph. (b)
State-space tree for finding a Hamiltonian circuit. The numbers above the nodes
of the tree indicate the order in which the nodes are generated.
KNAPSACK PROBLEM
The
knapsack problem or rucksack problem is a problem in combinatorial
optimization: Given a set of items, each with a weight and a value, determine
the number of each item to include in a collection so that the total weight is
less than a given limit and the total value is as large as possible.
It
derives its name from the problem faced by someone who is constrained by a
fixed-size knapsack and must fill it with the most useful items.
The
problem often arises in resource allocation with financial constraints. A
similar problem also appears in combinatorics, complexity theory, cryptography
and applied mathematics.
The
decision problem form of the knapsack problem is the question "can a value
of at least V be achieved without exceeding the weight W?"
E.g. A
thief enters a store and sees the following items:
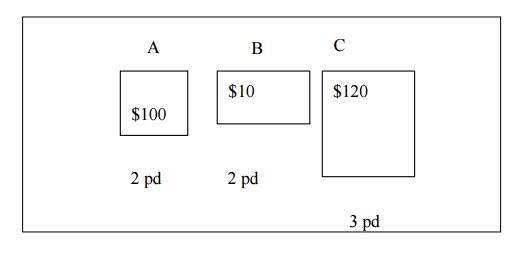
His
Knapsack holds 4 pounds.
What
should he steal to maximize profit?
Fractional
Knapsack Problem
Thief can
take a fraction of an item.
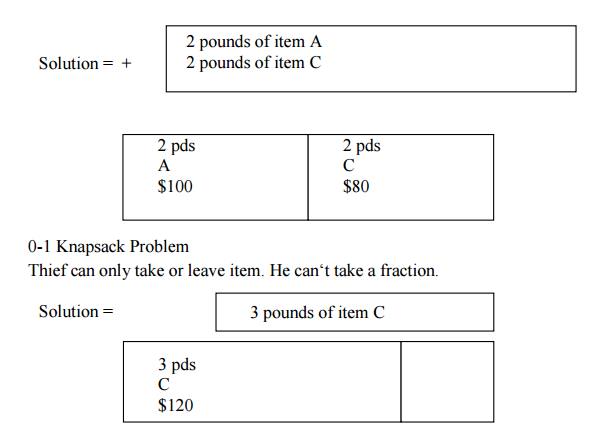
Fractional
Knapsack has a greedy solution
Sort
items by decreasing cost per pound

Related Topics