Subset- Sum problem

SUBSET-SUM PROBLEM

Subset-Sum Problem is finding a subset of a given set S = {s1,s2….sn} of n positive integers whose sum is equal to a given positive integer d.

For example, for S = {1, 2, 5, 6, 8) and d = 9, there are two solutions: {1, 2, 6} and {1, 8}. Of course, some instances of this problem may have no solutions.

that s1 ≤ s2 ≤ ……. ≤ sn

The state-space tree can be constructed as a binary tree as that in the following figure for the instances S = (3, 5, 6, 7) and d = 15.

The root of the tree represents the starting point, with no decisions about the given elements made as yet.

Its left and right children represent, respectively, inclusion and exclusion ofs1 in a set being sought.

Similarly, going to the left from a node of the first level corresponds to inclusion of s2, while going to the right corresponds to its exclusion, and soon.

Thus, a path from the root to a node on the ith level of the tree indicates which of the first i numbers have been included in the subsets represented by that node.

We record the value of s‘ the sum of these numbers, in the node, Ifs is equal to d. we have a solution to the problem.

We can either, report this result and stop or, if all the solutions need to he found, continue by backtracking to the node‘s parent.

If s‘ is not equal to d, we can terminate the node as nonpromising if either of the two inequalities holds:

1. Pseudocode For Backtrack Algorithms

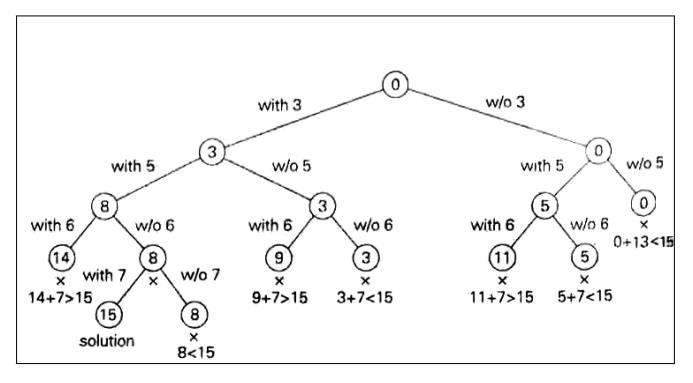
Fig: Complete state-space tree of the backtracking algorithm

(applied to the instance S = (3, 5, 6, 7) and d = 15 of the subset-sum problem. The number inside a node is the sum of the elements already included in subsets represented by the node. The inequality below a leaf indicates the reason for its termination)