Chapter: Essential Microbiology: Microbial Growth
The kinetics of microbial growth
The kinetics of microbial growth
Unicellular organisms divide by binary fission; each cell grows to full size, replicates its genetic material then divides into two identical daughter cells. By identical means, two cells divide into four, four into eight and so on, leading to an exponential increase in cell numbers:
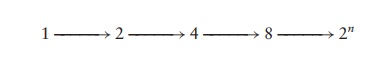
If we were to plot the number of cells in a population against time, we would get an exponential curve (Figure 5.8a). It is more convenient when plotting a growth curve
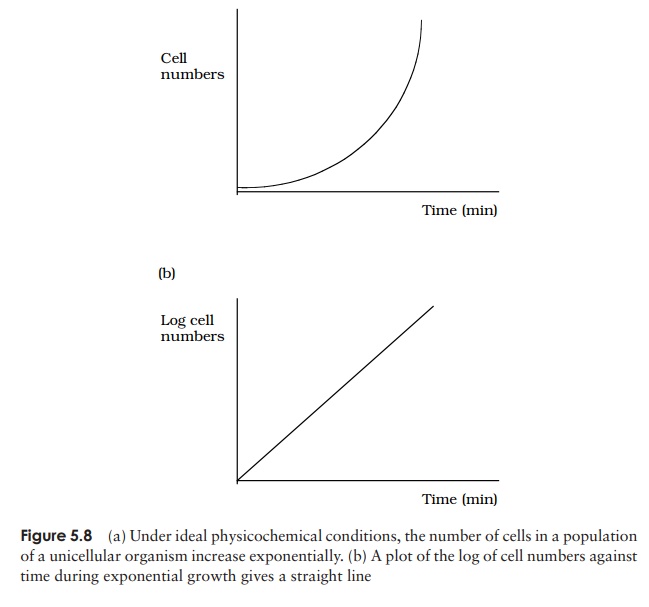
to plot the logarithm of cell numbers of against time, giving us a straight line (Fig-ure 5.8b). Such exponential growth cannot continue indefinitely, however, and growth usually slows down due to either the supply of nutrients becoming exhausted, or be-cause metabolism leads to an accumulation of harmful waste substances. Unicellular growth usually occurs in a series of different phases (Figure 5.9):
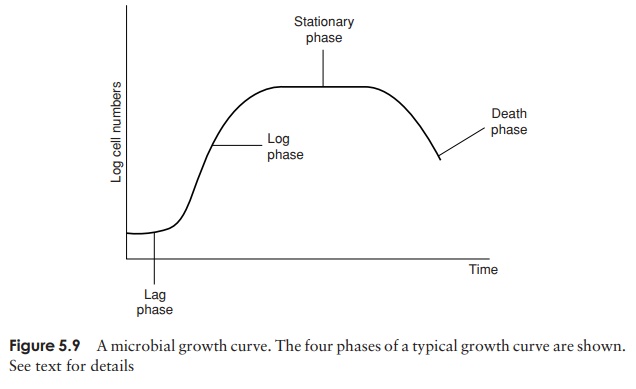
1. Lag phase. When an inoculum of bacteria is first in-troduced into some growth medium, it will probably require a period to adapt to its new surroundings – the less familiar these are, the longer the period of adaptation. If, for example, the carbon source in the medium is unfamiliar, the cells will need time to synthesise the necessary enzymes for its metabolism. The length of the lag phase will also depend on the age and general health of the cells in the inoculum. During this period, there is no net increase in bacterial numbers, however the cells are metabolically active.
2. Log (exponential) phase. When the bacteria have acclimatised to their new environ-ment and synthesised the enzymes needed to utilise the available substrates, they are able to start regular division by binary fission. This leads to the exponential increase in numbers referred to above. Under optimal conditions, the population of cells will double in a constant and predictable length of time, known as the gener-ation (doubling) time. The value for the widely used laboratory bacterium E. coli is 20 min, and for most organisms it is less than an hour. There are some bacteria, however, whose generation time is many hours. Thus, during exponential growth, the number of cells can be expressed as:
NT= N0×2n
whereN0 is the number of cells at the start of exponential growth, NT is the number of cells after time T, L is the length of the lag phase and n is the number of doubling times that have elapsed. n is therefore equal to T/Td, where Td is the doubling time. Substituting into the first equation:
NT= N0×2T/Td
This can be expressed more conveniently by using logarithms to the base 2 (don’t worry too much about how this is done!):
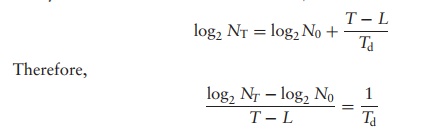
Thus, if we know the number of cells at the start and end of a period of exponential growth, we can calculate the doubling time. We can also determine the mean growth rate constant (K); this is a measure of the number of doublings of the population per unit time, and is equal to 1/Td∗ .
Many antibiotics such as penicillin are only effective when cells are actively dividing, since they depend on disrupting new cell wall synthesis.
3. Stationary phase. As discussed above, the exponential phase is limited by environ-mental factors, and as the rate of growth slows down, the culture enters the next phase. The levelling out of the growth curve does not mean that cell division has ceased completely, but rather that the increase due to newly formed cells is can-celled out by a similar number of cell deaths. Eventually, however, as the death rate increases, the overall numbers fall and we enter the final phase of growth.
4. Death phase. As cells die off and the culture is unable to replace them, the totalpopulation of viable cells falls. This is the death (or decline) phase.
Batch culture and continuous culture
The phases of growth described above apply to a batch culture. In this form of culture, appropriate nutrients and other conditions are provided for growth, then an inoculum is added and the culture incubated. No further nutrients are added and no waste prod-ucts are removed, thus conditions in the culture are continually changing. This results in active growth being of limited duration for the reasons outlined above.
Sometimes it is desirable to keep the culture in the logarithmic phase, for example if the cells are being used to produce alcohol or antibiotics. In a continuous culture, nutrient concentrations and other conditions are held constant, and the cells are held in a state of exponential growth. This is achieved by continuously adding fresh culture medium and removing equal volumes of the old. Parameters such as pH can also be mon-itored and adjusted. The equipment used to do this is called a chemostat (Figure 5.10); it
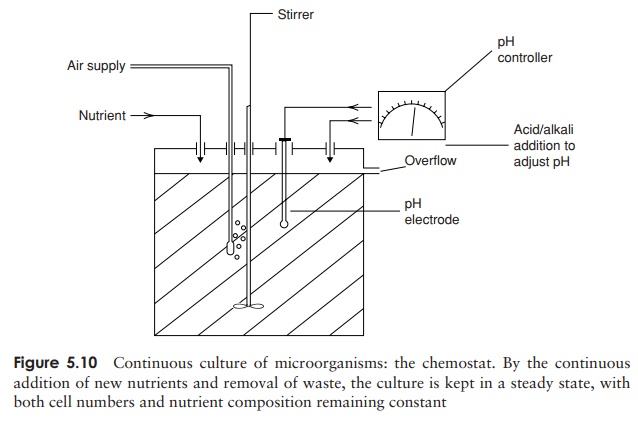
Related Topics