The Insertion Sort

The Insertion Sort

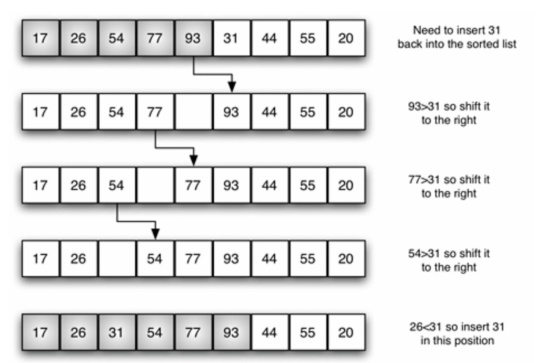
The insertion sort, although still (O(n^{2})\), works in a slightly different way. It always maintains a sorted sublist in the lower positions of the list. Each new item is then “inserted” back into the previous sublist such that the sorted sublist is one item larger. The figure below shows the insertion sorting process. The shaded items represent the ordered sublists as the algorithm makes each pass. We begin by assuming that a list with one item (position \(0\)) is already sorted. On each pass, one for each item 1 through \(n-1\), the current item is checked against those in the already sorted sublist. As we look back into the already sorted sublist, we shift those items that are greater to the right. When we reach a smaller item or the end of the sublist, the current item can be inserted. The figure below shows the fifth pass in detail. At this point in the algorithm, a sorted sublist of five items consisting of 17, 26, 54, 77, and 93 exists. We want to insert 31 back into the already sorted items. The first comparison against 93 causes 93 to be shifted to the right. 77 and 54 are also shifted. When the item 26 is encountered, the shifting process stops and 31 is placed in the open position. Now we have a sorted sublist of six items.

The implementation of insertionSort (ActiveCode 4) shows that there are again \(n- 1\) passes to sort nitems. The iteration starts at position 1 and moves through position \(n-1\), as these are the items that need to be inserted back into the sorted sublists. Line 8 performs the shift operation that moves a value up one position in the list, making room behind it for the insertion. Remember that this is not a complete exchange as was performed in the previous algorithms.

The maximum number of comparisons for an insertion sort is the sum of the first (n- 1\) integers. Again, this is \(O(n^{2})\). However, in the best case, only one comparison needs to be done on each pass. This would be the case for an already sorted list. One note about shifting versus exchanging is also important. In general, a shift operation requires approximately a third of the processing work of an exchange since only one assignment is performed. In benchmark studies, insertion sort will show very good performance.

PSEUDOCODE for INSERTION SORT: def insertionSort(alist):

for index in range(1,len(alist)): currentvalue = alist[index] position = index

while position>0 and alist[position-1]>currentvalue: alist[position]=alist[position-1]

position = position-1 alist[position]=currentvalue

alist = [54,26,93,17,77,31,44,55,20] insertionSort(alist)

print(alist)