Chapter: Object Oriented Programming and Data Structure : Sorting And Searching
Brief note on Merge Sort
Give a brief note on Merge Sort
We now
turn our attention to mergesort.
Mergesort runs in O(N logN)
worst-case running time, and the number of comparisons used is nearly optimal.
It is a fine example of a recursive algorithm. The fundamental operation in
this algorithm is merging two sorted lists. Because the lists are sorted, this
can be done in one pass through the input, if the output is put in a third
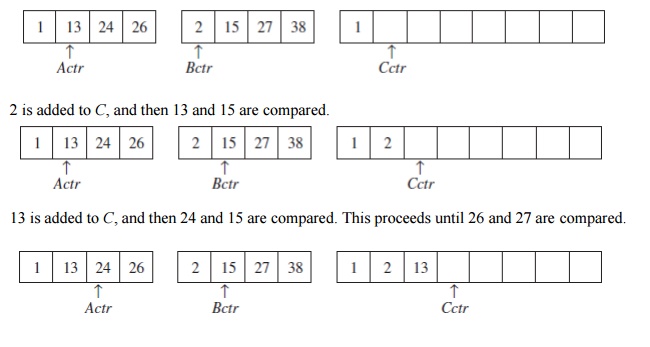
list. The basic merging algorithm takes two input arrays A and B, an output array C, and three counters, Actr, Bctr, and Cctr, which are
initially set to the beginning of their respective arrays. The smaller of A[Actr]
and B[Bctr] is copied to the next entry in C, and the appropriate counters are advanced. When either input
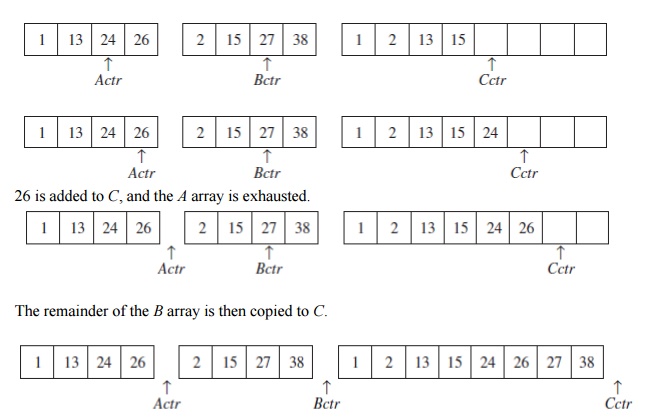
list is exhausted, the remainder of the other list is copied to C. An example of how the merge routine
works is provided for the following input.

If the
array A contains 1, 13, 24, 26, and B contains 2, 15, 27, 38, then the
algorithm proceeds as follows: First, a comparison is done between 1 and 2. 1
is added to C, and then 13 and 2 are
compared.
The time
to merge two sorted lists is clearly linear, because at most N−1 comparisons are made, where N is the total number of elements. To
see this, note that every comparison adds an element to C, except the last comparison, which adds at least two. The
mergesort algorithm is therefore easy to describe. If N = 1, there is only one element to sort, and the answer is at
hand. Otherwise, recursively mergesort the first half and the second half. This
gives two sorted halves, which can then be merged together using the merging
algorithm described above. For instance, to sort the eight-element array 24,
13, 26, 1, 2, 27, 38, 15, we recursively sort the first four and last four
elements, obtaining 1, 13, 24, 26, 2, 15, 27, 38. Then we merge the two halves
as above, obtaining the final list 1, 2, 13, 15, 24, 26, 27, 38. This algorithm
is a classic divide-and-conquer strategy. The problem is divided into smaller problems and solved recursively. The conquering phase consists of patching
together the answers. Divide-and-conquer is a very powerful use of recursion
that we will see many times. An implementation of mergesort is provided. The
one-parameter mergeSort is just a driver for the four-parameter recursive
mergeSort. The merge routine is subtle. If a temporary array is declared
locally for each recursive call of merge, then there could be logN temporary arrays active at any point.
A close examination shows that since merge is the last line of mergeSort, there
only needs to be one
1 /**
2 *
Mergesort algorithm (driver).
3 */
4 template
<typename Comparable>
5 void
mergeSort( vector<Comparable> & a )
6 {
7 vector<Comparable>
tmpArray( a.size( ) );
8
9 mergeSort(
a, tmpArray, 0, a.size( ) - 1 );
10}
11
12/**
13* Internal method that makes
recursive calls.
14* a is an array of Comparable
items.
15* tmpArray is an array to place
the merged result.
16* left is the left-most index of
the subarray.
17* right is the right-most index
of the subarray.
18*/
19template <typename
Comparable>
20void mergeSort(
vector<Comparable> & a,
21vector<Comparable> &
tmpArray, int left, int right )
22{
23if( left < right )
24{
25int center = ( left + right ) /
2;
26mergeSort( a, tmpArray, left,
center );
27mergeSort( a, tmpArray, center +
1, right );
28merge( a, tmpArray, left, center
+ 1, right );
29}
30}
Mergesort routines
temporary
array active at any point, and that the temporary array can be created in the
public mergeSort driver. Further, we can use any part of the temporary array;
we will use the same portion as the input array a.
Analysis of Mergesort
Mergesort
is a classic example of the techniques used to analyze recursive routines: We
have to write a recurrence relation for the running time. We will assume that N is a power of 2 so that we always
split into even halves. For N = 1,
the time to mergesort is constant, which we will denote by 1. Otherwise, the
time to mergesort N numbers is equal
to the
1 /**
2 *
Internal method that merges two sorted halves of a subarray.
3 * a is an
array of Comparable items.
4 *
tmpArray is an array to place the merged result.
5 * leftPos
is the left-most index of the subarray.
6 *
rightPos is the index of the start of the second half.
7 *
rightEnd is the right-most index of the subarray.
8 */
9 template
<typename Comparable>
10 void
merge( vector<Comparable> & a, vector<Comparable> &
tmpArray,
11 int
leftPos, int rightPos, int rightEnd )
12 {
13 int
leftEnd = rightPos - 1;
14 int
tmpPos = leftPos;
15 int numElements
= rightEnd - leftPos + 1;
16
17 // Main
loop
18 while(
leftPos <= leftEnd && rightPos <= rightEnd ) 19 if( a[ leftPos ] <= a[ rightPos ] )
20 tmpArray[
tmpPos++ ] = std::move( a[ leftPos++ ] );
21 else
22 tmpArray[
tmpPos++ ] = std::move( a[ rightPos++ ] );
23
24 while(
leftPos <= leftEnd ) // Copy rest of first half
25 tmpArray[
tmpPos++ ] = std::move( a[ leftPos++ ] );
26
27 while(
rightPos <= rightEnd ) // Copy rest of right half
28 tmpArray[
tmpPos++ ] = std::move( a[ rightPos++ ] );
29
30 // Copy
tmpArray back
31 for( int
i = 0; i < numElements; ++i, --rightEnd )
32 a[
rightEnd ] = std::move( tmpArray[ rightEnd ] );
33 }
merge routine
time to
do two recursive mergesorts of size N/2,
plus the time to merge, which is linear. The following equations say this
exactly:
T(1) = 1
T(N) = 2T(N/2) + N
This is a
standard recurrence relation, which can be solved several ways.We will show two
methods. The first idea is to divide the recurrence relation through by N. The reason for doing this will become
apparent soon. This yields
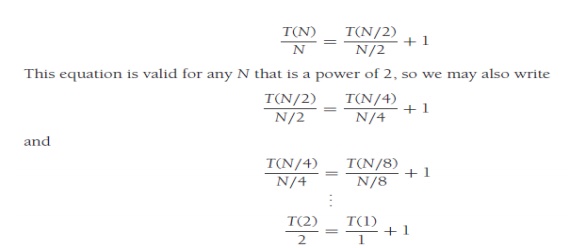
Now add up all the equations. This means that we add all of the terms on the left-hand side and set the result equal to the sum of all of the terms on the right-hand side. Observe that the term T(N/2)/(N/2) appears on both sides and thus cancels. In fact, virtually all the terms appear on both sides and cancel. This is called telescoping a sum. After everything is added, the final result is
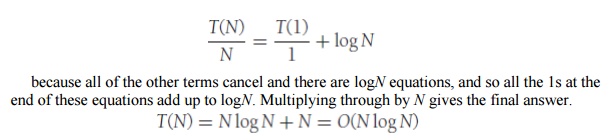
Notice that if we did not divide through by N at the start of the solutions, the sum would not telescope. This is why it was necessary to divide through by N. An alternative method is to substitute the recurrence relation continually on the righthand side. We have

The
choice of which method to use is a matter of taste. The first method tends to
produce scrap work that fits better on a standard 81/2 × 11 sheet of paper leading to fewer mathematical errors, but it
requires a certain amount of experience to apply. The second method is more of
a brute-force approach. Recall that we have assumed N = 2k. The analysis can
be refined to handle cases
when N is not a power of 2. The answer turns
out to be almost identical (this is usually the case). Although mergesort’s
running time is O(N logN),
it has the significant problem that merging two
sorted
lists uses linear extra memory. The additional work involved in copying to the
temporary array and back, throughout the algorithm, slows the sort
considerably. This copying can be avoided by judiciously switching the roles of
a and tmpArray at alternate levels of the recursion. A variant of mergesort can
also be implemented nonrecursively.
The
running time of mergesort, when compared with other O(N logN) alternatives, depends heavily on the
relative costs of comparing elements and moving elements in the array (and the
temporary array). These costs are language dependent. For instance, in Java,
when performing a generic sort (using a Comparator), an element comparison can
be expensive (because comparisons might not be easily inlined, and thus the
overhead of dynamic dispatch could slow things down), but moving elements is
cheap (because they are reference assignments, rather than copies of large
objects). Mergesort uses the lowest number of comparisons of all the popular
sorting algorithms, and thus is a good candidate for general-purpose sorting in
Java. In fact, it is the algorithm used in the standard Java library for
generic sorting. On the other hand, in classic C++, in a generic sort, copying
objects can be expensive if the objects are large, while comparing objects
often is relatively cheap because of the ability of the compiler to
aggressively perform inline optimization. In this scenario, it might be
reasonable to have an algorithm use a few more comparisons, if we can also use
significantly fewer data movements
Related Topics