Detail about Insertion Sort

Discuss in detail about Insertion Sort

One of the simplest sorting algorithms is the insertion sort. Insertion sort consists of N−1 passes. For pass p=1 through N−1, insertion sort ensures that the elements in positions 0 through p are in sorted order. Insertion sort makes use of the fact that elements in positions 0 through p−1 are already known to be in sorted order. Figure below shows a sample array after each pass of insertion sort. Figure belowshows the general strategy. In pass p, we move the element in position p left until its correct place is found among the first p+1 elements. The code implements this strategy. Lines 11 to 14 implement that data movement without the explicit use of swaps.

The element in position p is moved to tmp, and all larger elements (prior to position p) are moved one spot to the right. Then tmp is moved to the correct spot. This is the same technique that was used in the implementation of binary heaps.

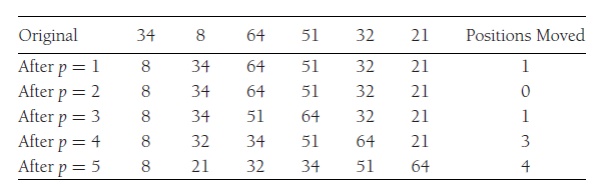
Insertion Sort After each Pass

1 /**

2 * Simple insertion sort.

3 */

4 template <typename Comparable>

5 void insertionSort( vector<Comparable> & a )

6 {

7 for( int p = 1; p < a.size( ); ++p )

8 {

9 Comparable tmp = std::move( a[ p ] );

10

11 int j;

12 for( j = p; j > 0 && tmp < a[ j - 1 ]; --j ) 13 a[ j ] = std::move( a[ j - 1 ] );

14 a[ j ] = std::move( tmp );

15}

16}

Insertion sort routine

Implementation of Insertion Sort

In the STL, instead of having the sort routines take an array of comparable items as a single parameter, the sort routines receive a pair of iterators that represent the start and endmarker of a range. A two-parameter sort routine uses just that pair of iterators and presumes that the items can be ordered, while a three-parameter sort routine has a function object as a third parameter. Converting the algorithm in Figure 7.2 to use the STL introduces several issues. The obvious issues are

1.   We must write a two-parameter sort and a three-parameter sort. Presumably, the two parameter sort invokes the three-parameter sort, with less<Object>{ } as the third parameter.

2.   Array access must be converted to iterator access.

3. Line 11 of the original code requires that we create tmp, which in the new code will have type Object.

The first issue is the trickiest because the template type parameters (i.e., the generic types) for the two-parameter sort are both Iterator; however, Object is not one of the generic type parameters. Prior to C++11, one had to write extra routines to solve this problem. As shown in Figure 7.3, C++11 introduces decltype which cleanly expresses the intent. Algorithm shows the main sorting code that replaces array indexing with use of the iterator, and that replaces calls to operator< with calls to the lessThan function object. Observe that once we actually code the insertionSort algorithm, every statement in the original code is replaced with a corresponding statement in the new code that makes

1  /*

2  * The two-parameter version calls the three-parameter version,

3  * using C++11 decltype

4  */

5  template <typename Iterator>

6  void insertionSort( const Iterator & begin, const Iterator & end )

7  {

8  insertionSort( begin, end, less<decltype(*begin)>{ } );

9  }

Two-parameter sort invokes three-parameter sort via C++11 decltype

1 template <typename Iterator, typename Comparator>

2 void insertionSort( const Iterator & begin, const Iterator & end, 3 Comparator lessThan )

4  {

5  if( begin == end )

6  return;

7

8 Iterator j;

9

10 for( Iterator p = begin+1; p != end; ++p )

11 {

12 auto tmp = std::move( *p );

13 for( j = p; j != begin && lessThan( tmp, *( j-1 ) ); --j )

14 *j = std::move( *(j-1) );

15 *j = std::move( tmp );

16 }

17 }

Three-parameter sort using iterators

straightforward use of iterators and the function object. The original code is arguably much simpler to read, which is why we use our simpler interface rather than the STL interface when coding our sorting algorithms.

Analysis of Insertion Sort

Because of the nested loops, each of which can take N iterations, insertion sort is O(N2). Furthermore, this bound is tight, because input in reverse order can achieve this bound. A precise calculation shows that the number of tests in the inner loop in is at most p + 1 for each value of  p.

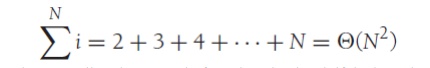
Summing over all p gives a total of On the other hand, if the input is presorted, the running time is O(N), because the test in the inner for loop always fails immediately. Indeed, if the input is almost sorted (this term will be more rigorously defined in the next section), insertion sort will run quickly. Because of this wide variation, it is worth analyzing the average-case behavior of this algorithm. It turns out that the average case is _(N2) for insertion sort, as well as for a variety of other sorting algorithms.