The Dag Representation For Basic Blocks

THE DAG REPRESENTATION FOR BASIC BLOCKS

•   A DAG for a basic block is a directed acyclic graph with the following labels on nodes:

1.   Leaves are labeled by unique identifiers, either variable names or constants.

2.   Interior nodes are labeled by an operator symbol.

3.   Nodes are also optionally given a sequence of identifiers for labels to store the computed values.

•   DAGs are useful data structures for implementing transformations on basic blocks.

•   It gives a picture of how the value computed by a statement is used in subsequent statements.

•   It provides a good way of determining common sub - expressions.

Algorithm for construction of DAG

Input: A basic block

Output: A DAG for the basic block containing the following information:

1.    A label for each node. For leaves, the label is an identifier. For interior nodes, an operator symbol.

2.   For each node a list of attached identifiers to hold the computed values. Case (i) x : = y OP z Case (ii) x : = OP y

Case (iii) x : = y

Method:

Step 1:

If y is undefined then create node(y).

If z is undefined, create node(z) for case(i).

Step 2:

For the case(i), create a node(OP) whose left child is node(y) and right child is node(z). (Checking for common sub expression). Let n be this node.

For case(ii), determine whether there is node(OP) with one child node(y). If not create such a node.

For case(iii), node n will be node(y).

Step 3:

Delete x from the list of identifiers for node(x). Append x to the list of attached identifiers for the node n found in step 2 and set node(x) to n.

Example: Consider the block of three- address statements in Fig 4.6

Stages in DAG Construction

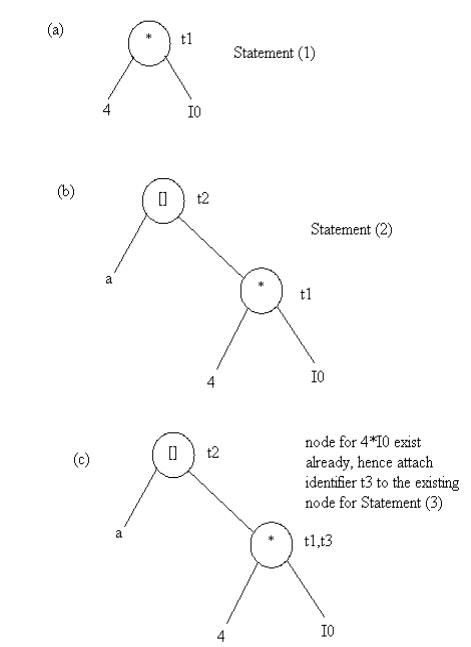
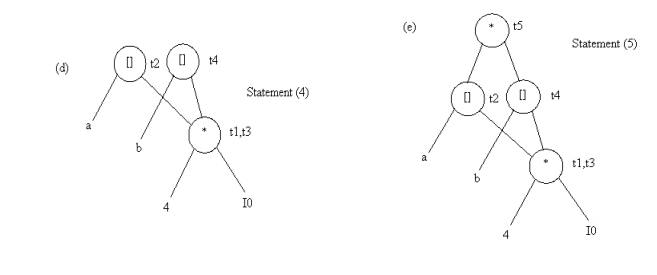
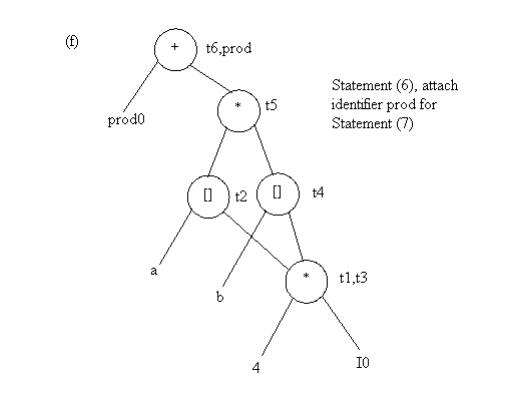
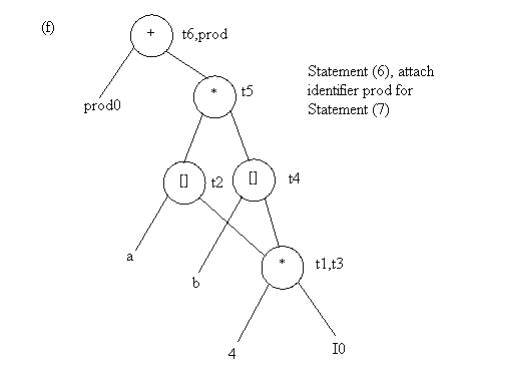
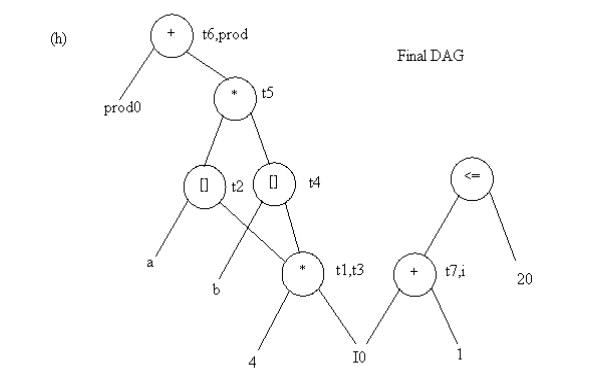
Fig. 4.5 Steps in DAG construction process

 Fig. 4.6 Code Block

Application of DAGs:

1.   We can automatically detect common sub expressions.

2.   We can determine which identifiers have their values used in the block.

3.   We can determine which statements compute values that could be used outside the block.