Generating Code From DAGs

GENERATING CODE FROM DAGs

The advantage of generating code for a basic block from its dag representation is that from a dag we can easily see how to rearrange the order of the final computation sequence than we can start from a linear sequence of three-address statements or quadruples.

Rearranging the order

The order in which computations are done can affect the cost of resulting object code. For example, consider the following basic block:

t1 : = a + b

t2 : = c + d

t3 : = e - t2

t4 : = t1 - t3

Generated code sequence for basic block:

MOV a , R0

ADD b , R0

MOV c , R1

ADD d , R1

MOV R0 , t1

MOV e , R0

SUB R1 , R0

MOV t1 , R1

SUB R0 , R1

MOV R1 , t4

Rearranged basic block:

Now t1 occurs immediately before t4.

t2 : = c + d

t3 : = e - t2

t1 : = a + b

t4 : = t1 - t3

Revised code sequence:

MOV c , R0

ADD d , R0

MOV a , R0

SUB R0 , R1

MOV a , R0

ADD b , R0

SUB R1 , R0

MOV R0 , t4

In this order, two instructions MOV R0 , t1 and MOV t1 , R1 have been saved.

A Heuristic ordering for Dags

The heuristic ordering algorithm attempts to make the evaluation of a nod the evaluation of its leftmost argument. The algorithm shown below produces the ordering in reverse.

Algorithm:

1)   while unlisted interior nodes remain do begin

2)                select an unlisted node n, all of whose parents have been listed;

3)                list n;

4)                while the leftmost child m of n has no unlisted parents and is not a leaf do

begin

5)                list m;

6)                n : = m

end

end

Example: Consider the DAG shown below

Initially, the only node with no unlisted parents is 1 so set n=1 at line (2) and list 1 at line (3). Now, the left argument of 1, which is 2, has its parents listed, so we list 2 and set n=2 at line (6). Now, at line (4) we find the leftmost child of 2, which is 6, has an unlisted parent 5. Thus we select a new n at line (2), and node 3 is the only candidate. We list 3 and proceed down its left chain, listing 4, 5 and 6. This leaves only 8 among the interior nodes so we list that. The resulting list is 1234568 and the order of evaluation is 8654321.

Code sequence:

t8 : = d + e

t6 : = a + b

t5 : = t6 - c

t4 : = t5 * t8

t3 : = t4 - e

t2 : = t6 + t4

t1 : = t2 * t3

This will yield an optimal code for the DAG on machine whatever be the number of registers.

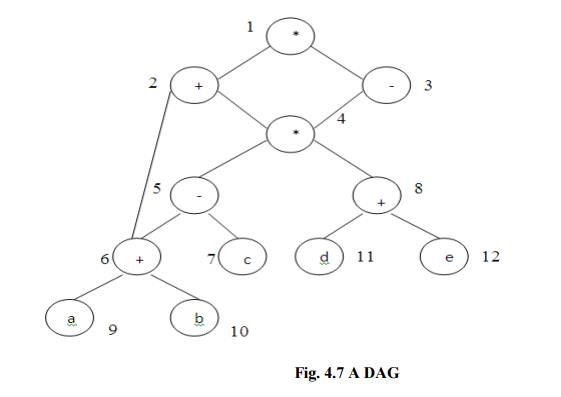
Fig. 4.7 A DAG