Testing for Primality

TESTING FOR PRIMALITY

For many cryptographic algorithms, it is necessary to select one or more very large prime numbers at random. Thus, we are faced with the task of determining whether a given large number is prime. There is no simple yet efficient means of accomplishing this task.

In this section, we present one attractive and popular algorithm. You may be surprised to learn that this algorithm yields a number that is not necessarily a prime. However, the algorithm can yield a number that is almost certainly a prime. This will be explained presently. We also make reference to a deterministic algo- rithm for finding primes. The section closes with a discussion concerning the distri- bution of primes.

Miller-Rabin Algorithm

The algorithm due to Miller and Rabin [MILL75, RABI80] is typically used to test a large number for primality. Before explaining the algorithm, we need some back- ground. First, any positive odd integer n >= 3 can be expressed as

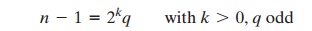
To see this, note that n - 1 is an even integer. Then, divide (n - 1) by 2 until the result is an odd number q, for a total of k divisions. If n is expressed as a binary num- ber, then the result is achieved by shifting the number to the right until the rightmost digit is a 1, for a total of k shifts. We now develop two properties of prime numbers that we will need.

TWO PROPERTIES OF PRIME NUMBERS The first property is stated as follows: If p is prime and a is a positive integer less than p, then a2 mod p  =  1 if and only if either a mod p =  1 or a mod p =  -1 mod p =  p - 1. By the rules of modular  arithmetic (a mod p) (a mod p)  = a2 mod p.  Thus,  if  either a mod p = 1 or a mod p = -1, then a2 mod p = 1. Conversely, if a2 mod p = 1, then (a mod p)2 = 1, which is true only for a mod p =  1 or a mod p = -1

The second property is stated as follows: Let p be a prime number greater  than 2. We can then write p - 1 = 2kq with k  >  0,  q odd. Let a be any integer in  the range 1  <  a <  p - 1. Then one of the two following conditions is  true.

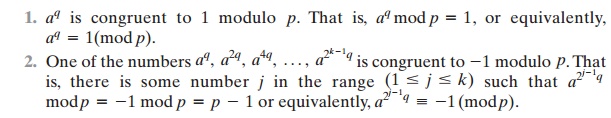
Proof: Fermat’s theorem [Equation (8.2)] states that an - 1 == 1 (mod n) if n is prime. We have p - 1 = 2kq. Thus, we know that ap - 1 mod p = a2 q mod p = 1. Thus, if we look at the sequence of numbers

we know that the last number in the list has value 1. Further, each number in the list is the square of the previous number. Therefore, one of the following possibilities must be true.

1.                                                                               The first number on the list, and therefore all subsequent numbers on the list, equals 1.

2.                                                                               Some number on the list does not equal 1, but its square mod p does equal 1. By virtue of the first property of prime numbers defined above, we know that the only number that satisfies this condition is p - 1. So, in this case, the list contains an element equal to p - 1.

This completes the proof.

DETAILS OF THE ALGORITHM These considerations lead to the conclusion that, if n is prime,  then  either  the  first  element  in  the  list  of  residues,  or  remainders, (a^q, a^2q, ..... , a^2(k-1) q, a^2K q modulo n equals 1; or some element in the list equals (n - 1); otherwise n is composite (i.e., not a prime). On the other hand, if the condition is met, that does not necessarily mean that n is prime. For example, if   n = 2047 = 23 * 89, then n - 1 = 2 * 1023. We compute 2¹⁰²³ mod 2047 = 1, so that 2047 meets the condition but is not prime.

 We can use the preceding property to devise a test for primality. The procedure TEST takes a candidate integer n as input and returns the result composite if n is definitely not a prime, and the result inconclusive if n may or may not be a prime.

Let   us   apply    the    test    to    the    prime    number    n  =  29.    We    have   (n - 1)  =  28  =  22(7)  =  2kq.   First,   let   us    try    a =  10.    We    compute 107 mod 29 = 17, which is neither 1 nor 28, so we continue the test. The next calcu- lation finds that (107)2 mod 29 = 28, and the test returns inconclusive (i.e., 29 may be prime). Let’s try again with a =  2. We  have the following calculations:  27 mod 29 = 12; 214 mod 29 = 28; and the test again returns inconclusive. If we perform the test for all integers a in the range 1 through 28, we get the same inconclusive result, which is compatible with n being a prime number.

Now let us apply the test to the composite number n = 13 * 17 = 221. Then  (n -1) = 220  = 22(55)  = 2kq.  Let  us   try   a = 5.   Then   we   have 555 mod 221 = 112, which is neither 1 nor 220 (555)2 mod 221 = 168. Because we have used all values of j (i.e., j = 0 and j = 1) in line 4 of the TEST algorithm, the test returns composite, indicating that 221 is definitely a composite num- ber. But suppose we had selected a = 21. Then we have 2155 mod 221 = 200; (2155)2 mod 221 = 220; and the test returns inconclusive, indicating that 221 may be prime. In fact, of the 218 integers from 2 through 219, four of these will return an inconclusive result, namely 21, 47, 174, and 200.

REPEATED USE OF THE MILLER-RABIN ALGORITHM How can we use the Miller- Rabin algorithm to determine with a high degree of confidence whether or not an integer is prime? It can be shown [KNUT98] that given an odd number n that is not prime and a randomly chosen integer, a with 1 6 a 6 n - 1, the probability that TEST will return inconclusive (i.e., fail to detect that n is not prime) is less than 1/4. Thus, if t different values of a are chosen, the probability that all of them will pass TEST (return inconclusive) for n is less than (1/4)t. For example, for t = 10, the probability that a nonprime number will pass all ten tests is less than 10-6. Thus, for   a sufficiently large value of t, we can be confident that n is prime if Miller’s test always returns inconclusive.

This gives us a basis for determining whether an odd integer n is prime with a rea- sonable degree of confidence. The procedure is as follows: Repeatedly invoke TEST

(n) using randomly chosen values for a. If, at any point, TEST returns composite, then n is determined to be nonprime. If TEST continues to return inconclusive for t tests, then for a sufficiently large value of t, assume that n is prime.

A  Deterministic  Primality Algorithm

Prior to 2002, there was no known method of efficiently proving the primality of very large numbers. All of the algorithms in use, including the most popular (Miller-Rabin), produced a probabilistic result. In 2002, Agrawal, Kayal, and Saxena [AGRA02] developed a relatively simple deterministic algorithm that effi- ciently determines whether a given large number is a prime. The algorithm, known as the AKS algorithm, does not appear to be as efficient as the Miller-Rabin algorithm. Thus far, it has not supplanted this older, probabilistic technique [BORN03].

Distribution of Primes

It is worth noting how many numbers are likely to be rejected before a prime number is found using the Miller-Rabin test, or any other test for primality. A result from num- ber theory, known as the prime number theorem, states that the primes near n are spaced on the average one every (ln n) integers. Thus, on average, one would have to test on the order of ln(n) integers before a prime is found. Because all even integers can be immediately rejected, the correct figure is 0.5 ln(n). For example, if a prime on the order of magnitude of 2200 were sought, then about 0.5 ln(2200) = 69 trials would be needed to find a prime. However, this figure is just an average. In some places along the number line, primes are closely packed, and in other places there are large gaps.

The two consecutive odd integers 1,000,000,000,061 and 1,000,000,000,063 are both prime. On the other hand, 1001!  +  2, 1001!  +  3, ... , 1001!   +  1000, 1001!   + 1001 is a sequence of 1000 consecutive composite integers.