Fermat’s And Euler’s Theorems

FERMAT’S AND EULER’S THEOREMS

Two theorems that play important roles in public-key cryptography are Fermat’s theorem and Euler’s theorem.

Fermat’s Theorem

Fermat’s theorem states the following: If p is prime and a is a positive integer not divisible by p, then

Proof: Consider the set of positive integers less than p: {1, 2,  ......., p  -   1}  and multiply   each   element  by a,  modulo p,   to   get   the  set X = {a mod p,  2a mod p, ..... , (p - 1)a mod p}. None of the elements of X is equal to zero because p does not divide a. Furthermore, no two of the integers in X are equal. To see this, assume that ja == ka (mod p)), where 1 <= j < k <= p - 1. Because a is relatively prime5 to p, we can eliminate a from both sides of the equation [see Equation (4.3)] resulting in j === k (mod p). This last equality is impossible, because j and k are both positive integers less than p. Therefore, we know that the (p - 1) elements of X are all positive integers with no two elements equal. We can conclude the X consists of the set of integers {1, 2, ...., p - 1} in some order. Multiplying the numbers in both sets (p and X) and taking the result mod p yields

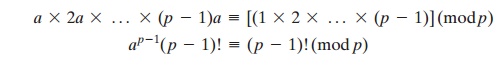
We can cancel the ((p - 1)! term because it is relatively prime to p [see Equation (4.5)]. This yields Equation (8.2), which completes the proof.

An alternative form of Fermat’s theorem is also useful: If p is prime and a is a positive  integer, then

Note that the first form of the theorem [Equation (8.2)] requires that a be relatively prime to p, but this form does not.

Euler’s Totient Function

Before presenting Euler’s theorem, we need to introduce an important quantity in number theory, referred to as Euler’s totient function, written Ï•(n), and defined as the number of positive integers less than n and relatively prime to n. By convention, Ï•(1)   =   1.

DETERMINE Ï•(37) AND Ï•(35).

Because 37 is prime, all of the positive integers from 1 through 36 are rela- tively prime to 37. Thus Ï•(37)   =   36.

To determine Ï•(35), we list all of the positive integers less than 35 that are rela- tively prime to it:

1, 2, 3, 4, 6, 8, 9, 11, 12, 13, 16, 17, 18

19, 22, 23, 24, 26, 27, 29, 31, 32, 33, 34

There are 24 numbers on the list, so Ï•(35)  =  24.

Table 8.2 lists the first 30 values of Ï•(n). The value Ï•(1) is without meaning but is defined to have the value 1.

It should be clear that, for a prime number p,

Ï•(p)  =  p  -  1

Now suppose that we have two prime numbers p and q with p != q. Then we can show that, for n = pq,

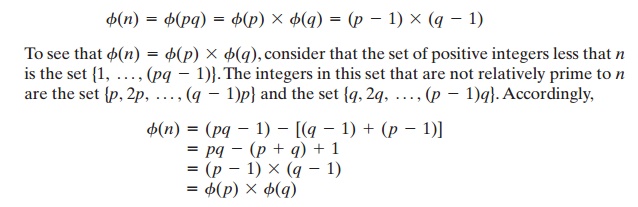
Euler’s Theorem

Euler’s theorem states that for every a and n that are relatively   prime:

Proof:   Equation (8.4) is true if n is prime, because in that case, Ï•(n)  =  (n  -  1) and Fermat’s theorem holds. However, it also holds for any integer n. Recall that f(n) is the number of positive integers less than n that are relatively prime to n. Consider the set of such integers, labeled as

R  =  {x1, x2,  ...... , xÏ•(n)}

That  is,  each  element xi is  a  unique  positive  integer  less  than  n with gcd(xi, n)  = 1. Now multiply each element by a, modulo n:

S  =  {(ax1 mod n), (ax2 mod n),  ....., (axÏ•(n) mod n)}

The set S is a permutation6 of R, by the following line of reasoning:

1.                                                                                  Because a is relatively prime to n and xi is relatively prime to n, axi must also be relatively prime to n. Thus, all the members of S are integers that are less than n and that are relatively prime to  n.

1. There are no duplicates in S. Refer to Equation (4.5). If axi mod n = axj mod n, then xi = xj.

Therefore,

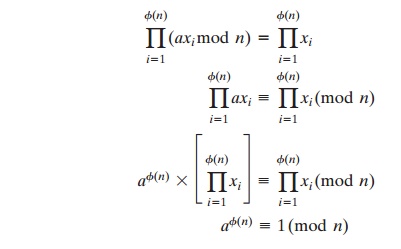
which completes the proof. This is the same line of reasoning applied to the proof of Fermat’s theorem.

As is the case for Fermat’s theorem, an alternative form of the theorem is also useful:

Again, similar to the case with Fermat’s theorem, the first form of Euler’s theorem [Equation (8.4)] requires that a be relatively prime to n, but this form does   not.