Prime Numbers

PRIME NUMBERS

A central concern of number theory is the study of prime numbers. Indeed, whole books have been written on the subject (e.g., [CRAN01], [RIBE96]). In this section, we provide an overview relevant to the concerns of this book.

An integer p  > 1 is a prime number if and only if its only divisors2 are ;1 and ; p. Prime numbers play a critical role in number theory and in the techniques discussed in this chapter. Table 8.1 shows the primes less than 2000. Note the way the primes are distributed. In particular, note the number of primes in each range of 100 numbers.

Any integer a > 1 can be factored in a unique way as

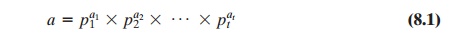
where p1 < p2 < ..... < pt are prime numbers and where each ai is a positive integer. This is known as the fundamental theorem of arithmetic; a proof can be found in any text on number theory.

91 = 7 * 13

3600 = 24 * 32 *  52

11011 = 7 * 112 *  13

It is useful for what follows to express this another way. If P is the set of all prime numbers, then any positive integer a can be written uniquely in the following form:

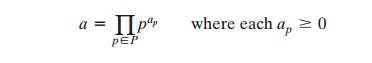
The right-hand side is the product over all possible prime numbers p; for any particular value of a, most of the exponents ap will be 0.

The value of any given positive integer can be specified by simply listing all the nonzero exponents in the foregoing formulation.

The integer 12 is represented by {a2 = 2, a3 =  1}. 

The integer 18 is represented by {a2 = 1, a3 =  2}. 

The integer 91 is represented by {a7  =  1,  a13  =  1}.

k = 12  * 18  = (22  * 3)  * (2  * 32)  =  216

k2  = 2  + 1  = 3; k3  = 1  + 2  =   3

216 = 23 * 33 = 8 *   27

What does it mean, in terms of the prime factors of a and b, to say that a divides b’ Any integer of the form pn  can be divided only by an integer that is of a lesser or equal power of the same prime number, pj with j … n. Thus, we can say the following.

Given

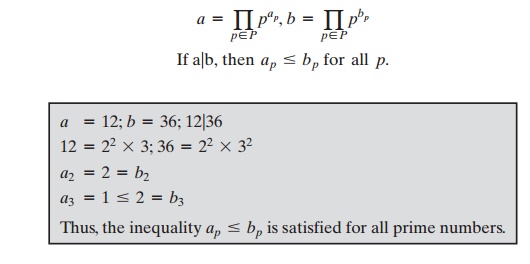
a   = 12; b = 36;  12|36

12 = 22 * 3; 36 = 22 *  32

a2  = 2  = b2

a3  = 1  … 2  =  b3

Thus, the inequality ap  … bp is satisfied for all prime numbers.

It is easy to determine the greatest common divisor3 of two positive integers if we express each integer as the product of primes.

300 = 22 * 31 *  52

18 = 21 * 32

gcd(18, 300) = 21 * 31 * 50 = 6

The following relationship always holds:

If k  =  gcd(a, b), then kp  = min(ap, bp) for all p.

Determining the prime factors of a large number is no easy task, so the pre- ceding relationship does not directly lead to a practical method of calculating the greatest common divisor.