Discrete Logarithms

DISCRETE LOGARITHMS

Discrete logarithms are fundamental to a number of public-key algorithms, includ- ing Diffie-Hellman key exchange and the digital signature algorithm (DSA). This section provides a brief overview of discrete logarithms. For the interested reader, more detailed developments of this topic can be found in [ORE67] and [LEVE90].

The Powers of an Integer, Modulo n

Recall from Euler’s theorem [Equation (8.4)] that, for every a and n that are rela- tively prime,

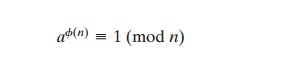
where Ï•(n), Euler’s totient function, is the number of positive integers less than n and relatively prime to n. Now consider the more general   expression:

If a and n are relatively prime, then there is at least one integer m that satisfies Equation  (8.10),  namely,  M  =  Ï•(n). The  least  positive  exponent  m  for  which Equation (8.10) holds is referred to in several ways:

•                           The order of a (mod n)

•                           The exponent to which a belongs (mod n)

•                           The length of the period generated by  a

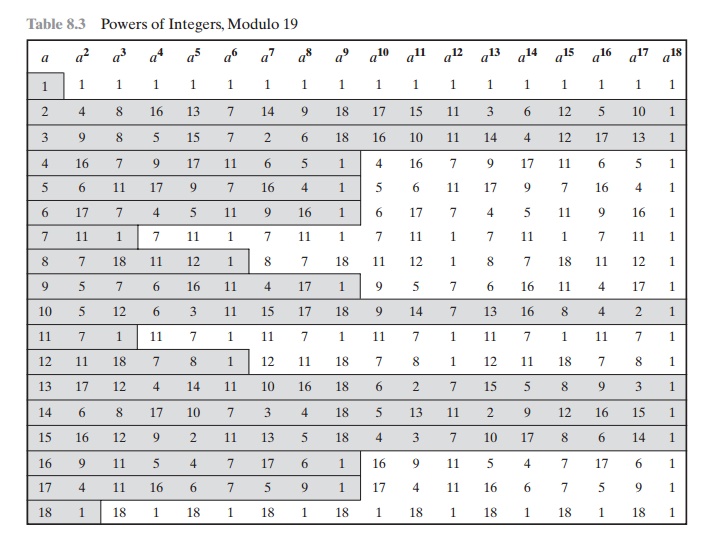
Table 8.3 shows all the powers of a, modulo 19 for all positive a 6 19. The length of the sequence for each base value is indicated by shading. Note the following:

1.                                                                               All sequences end in 1. This is consistent with the reasoning of the preceding few paragraphs.

2.                                                                               The length of a sequence divides Ï•(19)  =  18. That is, an integral number of sequences occur in each row of the table.

3.                                                                               Some of the sequences are of length 18. In this case, it is said that the base inte- ger a generates (via powers) the set of nonzero integers modulo 19. Each such integer is called a primitive root of the modulus 19.

More generally, we can say that the highest possible exponent to which a number can belong (mod n) is Ï•(n). If a number is of this order, it is referred to as a primitive root of n. The importance of this notion is that if a is a primitive root of n, then its powers

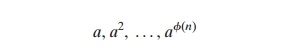
are distinct (mod n) and are all relatively prime to n. In particular, for a prime number p, if a is a primitive root of p, then

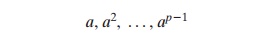
are distinct (mod p). For the prime number 19, its primitive roots are 2, 3, 10, 13,  14, and 15.

Not all integers have primitive roots. In fact, the only integers with primitive roots are those of the form 2, 4, pa, and 2pa, where p is any odd prime and a is a positive integer. The proof is not simple but can be found in many number theory books, including [ORE76].

Logarithms for Modular Arithmetic

With ordinary positive real numbers, the logarithm function is the inverse of expo- nentiation. An analogous function exists for modular arithmetic.

Let us briefly review the properties of ordinary logarithms. The logarithm of a number is defined to be the power to which some positive base (except 1) must be raised in order to equal the number. That is, for base x and for a value y,

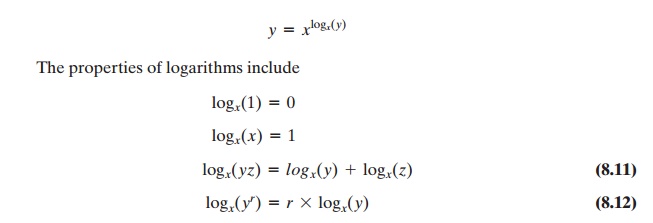
Consider a primitive root a for some prime number p (the argument can be developed for nonprimes as well). Then we know that the powers of a from 1 through (p - 1) produce each integer from 1 through (p - 1) exactly once. We also know that any integer b satisfies

by the definition of modular arithmetic. It follows that for any integer b and a prim- itive root a of prime number p, we can find a unique exponent i such that

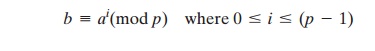
This exponent i is referred to as the discrete logarithm of the number b for the  base a (mod p). We denote this value as dloga,p(b).10

Note the following:

dloga,p(1) = 0 because a0 mod p = 1 mod p = 1            (8.13)

dloga,p(a)  =  1    because a1 mod p  =  a           (8.14)

This demonstrates the analogy between true logarithms and discrete logarithms.

Keep in mind that unique discrete logarithms mod m to some base a exist only if a is a primitive root of m.

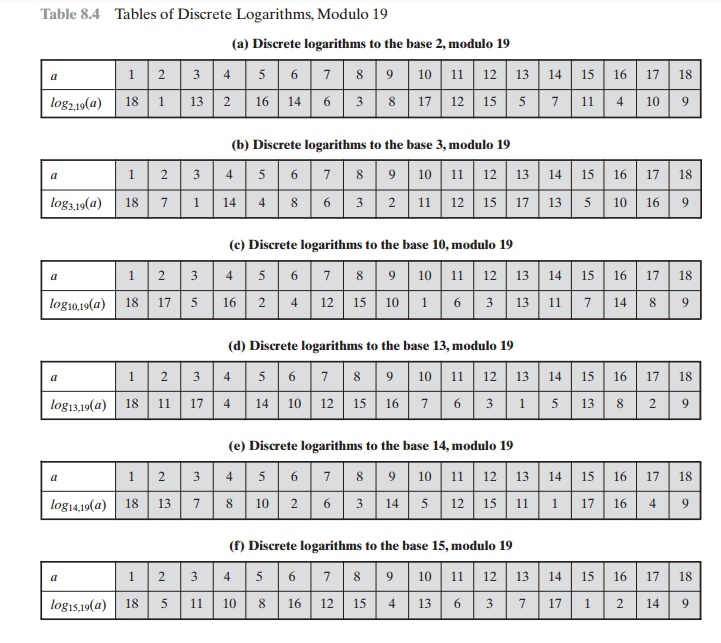
Table 8.4, which is directly derived from Table 8.3, shows the sets of discrete logarithms that can be defined for modulus 19.

Table 8.4    Tables of Discrete Logarithms, Modulo 19

Calculation of Discrete Logarithms

Consider the equation

y  =  gx mod p

Given g, x, and p, it is a straightforward matter to calculate y. At the worst, we must perform x repeated multiplications, and algorithms exist for achieving greater effi- ciency (see Chapter 9).

However, given y, g, and p, it is, in general, very difficult to calculate x (take the discrete logarithm). The difficulty seems to be on the same order of magnitude as that of factoring primes required for RSA. At the time of this writing, the asymptoti- cally fastest known algorithm for taking discrete logarithms modulo a prime number is on the order of [BETH91]:

e((ln p)1/3(ln(ln p))2/3))

which is not feasible for large primes.