Techniques to Improve QoS

Techniques to Improve QoS

Some techniques that can be used to improve the quality of service. The four common methods: scheduling, traffic shaping, admission control, and resource reservation.

a.  Scheduling

Packets from different flows arrive at a switch or router for processing. A good scheduling technique treats the different flows in a fair and appropriate manner. Several scheduling techniques are designed to improve the quality of service. We discuss three of them here: FIFO queuing, priority queuing, and weighted fair queuing.

i. FIFO Queuing

In first-in, first-out (FIFO) queuing, packets wait in a buffer (queue) until the node (router or switch) is ready to process them. If the average arrival rate is higher than the average processing rate, the queue will fill up and new packets will be discarded. A FIFO queue is familiar to those who have had to wait for a bus at a bus stop.

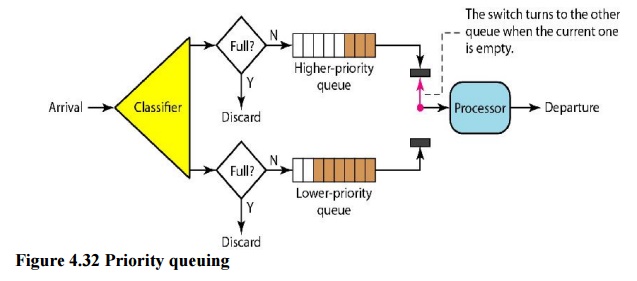
ii. Priority Queuing

In priority queuing, packets are first assigned to a priority class. Each priority class has its own queue. The packets in the highest-priority queue are processed first. Packets in the lowest- priority queue are processed last. Note that the system does not stop serving a queue until it is empty. Figure 4.32 shows priority queuing with two priority levels (for simplicity).

A priority queue can provide better QoS than the FIFO queue because higher priority traffic, such as multimedia, can reach the destination with less delay. However, there is a potential drawback. If there is a continuous flow in a high-priority queue, the packets in the lower-priority queues will never have a chance to be processed. This is a condition called starvation

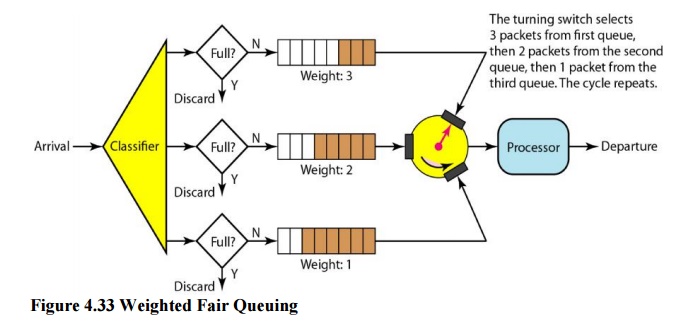
iii. Weighted Fair Queuing

A better scheduling method is weighted fair queuing. In this technique, the packets are still assigned to different classes and admitted to different queues. The queues, however, are weighted based on the priority of the queues; higher priority means a higher weight. The system processes packets in each queue in a round-robin fashion with the number of packets selected from each queue based on the corresponding weight. For example, if the weights are 3, 2, and 1, three packets are processed from the first queue, two from the second queue, and one from the third queue. If the system does not impose priority on the classes, all weights can be equal. In this way, we have fair queuing with priority. Figure 4.33 shows the technique with three classes.

b.  Traffic Shaping

Traffic shaping is a mechanism to control the amount and the rate of the traffic sent to the network. Two techniques can shape traffic: leaky bucket and token bucket

i. Leaky Bucket

If a bucket has a small hole at the bottom, the water leaks from the bucket at a constant rate as long as there is water in the bucket. The rate at which the water leaks does not depend on the rate at which the water is input to the bucket unless the bucket is empty. The input rate can vary, but the output rate remains constant. Similarly, in networking, a technique called leaky bucket can smooth out bursty traffic. Bursty chunks are stored in the bucket and sent out at an average rate. Figure 4.34 shows a leaky bucket and its effects.

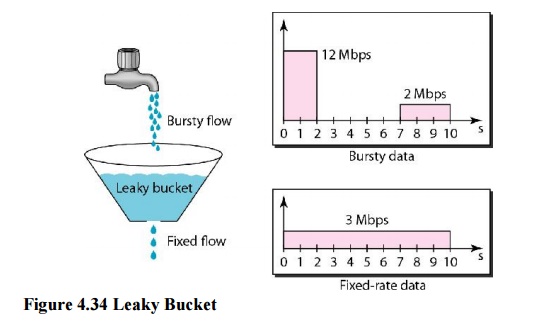
In the figure, we assume that the network has committed a bandwidth of 3 Mbps for a host. The use of the leaky bucket shapes the input traffic to make it conform to this commitment. In Figure 4.34 the host sends a burst of data at a rate of 12 Mbps for 2 s, for a total of 24 Mbits of data. The host is silent for 5 s and then sends data at a rate of 2 Mbps for 3 s, for a total of 6 Mbits of data. In all, the host has sent 30 Mbits of data in lOs. The leaky bucket smooth’s the traffic by sending out data at a rate of 3 Mbps during the same 10 s.

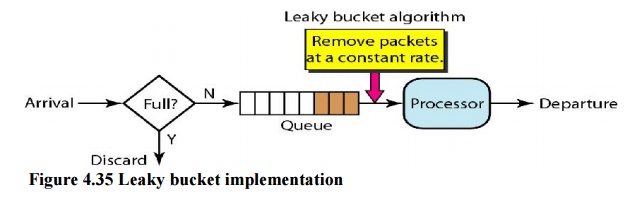
A simple leaky bucket implementation is shown in Figure 4.35. A FIFO queue holds the packets. If the traffic consists of fixed-size packets (e.g., cells in ATM networks), the process removes a fixed number of packets from the queue at each tick of the clock. If the traffic consists of variable-length packets, the fixed output rate must be based on the number of bytes or bits.

The following is an algorithm for variable-length packets:

·           Initialize a counter to n at the tick of the clock.

·           If n is greater than the size of the packet, send the packet and decrement the counter by the packet size. Repeat this step until n is smaller than the packet size.

·           Reset the counter and go to step 1.

A leaky bucket algorithm shapes bursty traffic into fixed-rate traffic by averaging the data rate. It may drop the packets if the bucket is full.

ii. Token Bucket

The leaky bucket is very restrictive. It does not credit an idle host. For example, if a host is not sending for a while, its bucket becomes empty. Now if the host has bursty data, the leaky bucket allows only an average rate. The time when the host was idle is not taken into account. On the other hand, the token bucket algorithm allows idle hosts to accumulate credit for the future in the form of tokens. For each tick of the clock, the system sends n tokens to the bucket. The system removes one token for every cell (or byte) of data sent. For example, if n is 100 and the host is idle for 100 ticks, the bucket collects 10,000 tokens.

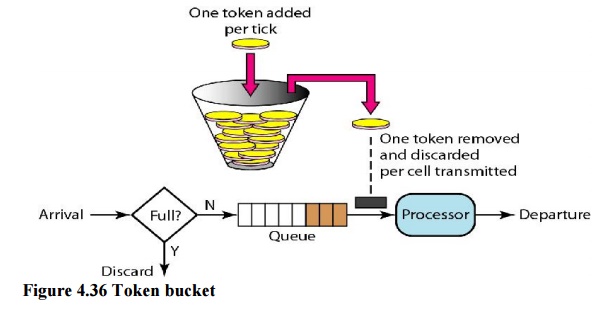
The token bucket can easily be implemented with a counter. The token is initialized to zero. Each time a token is added, the counter is incremented by 1. Each time a unit of data is sent, the counter is decremented by 1. When the counter is zero, the host cannot send data.

The token bucket allows bursty traffic at a regulated maximum rate.

Combining Token Bucket and Leaky Bucket

The two techniques can be combined to credit an idle host and at the same time regulate the traffic. The leaky bucket is applied after the token bucket; the rate of the leaky bucket needs to be higher than the rate of tokens dropped in the bucket.

c.  Resource Reservation

A flow of data needs resources such as a buffer, bandwidth, CPU time, and so on. The quality of service is improved if these resources are reserved beforehand. We discuss in this section one QoS model called Integrated Services, which depends heavily on resource reservation to improve the quality of service.

d.  Admission Control

Admission control refers to the mechanism used by a router, or a switch, to accept or reject a flow based on predefined parameters called flow specifications. Before a router accepts a flow for processing, it checks the flow specifications to see if its capacity (in terms of bandwidth, buffer size, CPU speed, etc.) and its previous commitments to other flows can handle the new flow.