System Models and Controllers Building

SYSTEM MODELS AND CONTROLLERS BUILDING

BLOCKS OF MECHANICAL SYSTEM:

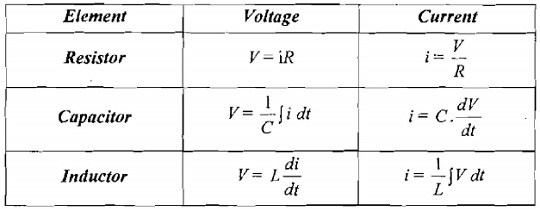
BLOCKS OF MECHANICAL SYSTEM:BUILDING BLOCKS OF ELECTRICAL SYSTEM:

TYPES OF CONTROL MODES:

The Two – Step Mode:

The two-step mode in which the controller is essentially just a switch which is activated by the error signal and supplied just an on-off correcting signal.

An example of the two-step mode of control is the bimetallic thermoset at that might be used with a simple temperature control system.

This is just a switch which is switched on or off according to the temperature then the bimetallic ship is in an off position and the heater is off.

If the room temperature falls below the required temperature then the bimetallic strip moves into an on position and the heater is switched fully on. The controller in this case

can be in only two positions, on or off.

The Proportional Mode (P):

The proportional mode (P) which products a control action that is proportional to the error. The correcting signal thus becomes bigger the bigger the error.

Thus as the error is reduced the amount of correction is reduced and the correcting process slows down.

The proportional mode, the size of the controller output is proportional to the size of the error.

K                                                            = 100 / Proportional Band

Change in Output (s)                              = K_p * E(s)

Transformer function                             = Change in Output (s) / E(s)

Electronic Proportional Controller:

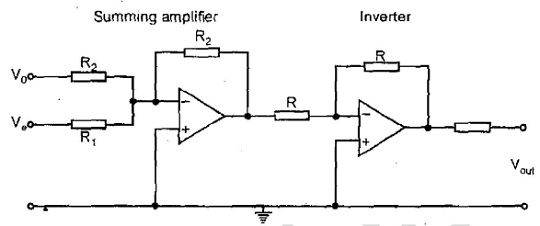
Example for Proportional Controller:

The Derivative Mode (D):

The derivative mode (D) which products a control action that is proportional to the rate at which are errors is changing.

When there is a sudden change in the error signal the controller gives a large correcting signal

When there is a gradual change only a small corrections signal is produced. Derivative control can be considered to be a form of anticipatory control in that the existing rate of

change of error is measured, a coming larger error is anticipated and correction applied

before the larger error has arrived.

Derivative mode of control the change in controller output from the set point value is proportional to the rate of change with time of the error signal

t – IO = KD

Proportional Plus Derivative Mode:

Change in output from the set point = K_P e + K_D

I_out = K_P e + K_D + I₀

The Integral Mode (I):

The integral mode (I) which produces a control action that is proportional to the integral of the error with time.

Thus a constant error signal will produce an increasing correcting signal. The correction continues to increase as long the error persists.

The integral mode of control is one where the rate of change of the control output I is proportional to the input error signal.

Proportional Plus Integral Control:

Iout = KP e + KI ∫ + IO

Transfer Function  = Kp +  =  (S +  )

Combinations of Modes:

Proportional plus derivative modes (PD), proportional plus integral modes (PI), proportional plus integral plus derivative modes (PID).

The term three – term controller is used for PID control.

DIGITAL CONTROLLERS:

The tern digital control is used when the digital controller, basically a microprocessor is in control of the closed-loop control system.

The controller receives inputs from sensors, executes control programs and provides the output to the correction elements.

The controllers require inputs which are digital, process the information in digital form and give an output in digital form.

Since many control systems have analogue measurements an analogue-to-digital converter (ADC) is used forth inputs.

A clock supplies a pulse at regular time intervals and dictates when samples of the controlled variable are taken by the ADC.

The  samples  are  then  converted  to  digital  signals  which  are  compared  by  the

microprocessor with the set point value to give the error signal.

The microprocessor can then initiate a control mode to process the error signal and give a digital output.

The control mode used by the microprocessor is determined by the program of instruction used by the microprocessor for processing the digital signals, i.e., the

software.

The digital output, generally after processing by a digital-to-analogue converter since correcting elements generally require analogue signals can be used to initiate the

correcting action

A digital controller basically operates the following cycle of events:

Samples the measured value.

Compares it with the set value and establishes the error.

Carries out calculations based on the error value and stored values of previous inputs and outputs to obtain the output signal

Sends the output signal to the DAC.

Waits until the next sample time before repeating the cycle.

VELOCITY CONTROL:

Consider the problem of controlling the movement of a load by means of a motor.

Time will thus be taken for the system to respond to an input signal.

A higher speed of respond, with fewer oscillations, can be obtained by using PD rather than just P control.

There is, however, alternative of achieving the same effect and this is by the use of a second feedback loop which gives a measurement related to the rate at which the

displacement is changing.

This is termed velocity feedback.

The velocity feedback might involve the use of a Tachogenerator giving a signal proportional to the rotational speed of the motor shaft and hence the rate at which the

displacement is changing and the displacement might be monitored using a rotary potentiometer

ADAPTIVE CONTROL:

An adaptive control system which 'adapts' to changes and changes its parameters to fit the circumstances prevailing.

The adaptive control system is based on the use of a microprocessor as the controller.

Such a device enables the control mode and the control parameters used to be adapted to fit the circumstances, modifying them as the circumstances change.

Stages of Adaptive Control System:

An adaptive control system can be considered to have three stages of operation.

Starts to operate with controller conditions set on the basis of an assumed condition.

The desired performance is continuously compared with the actual system performance.

The control system mode and parameters are automatically and continuously adjusted in order to minimise the difference between the desired and actual system performance.

Forms of Adaptive Control System:

Adaptive control systems can take a number of forms. Three commonly used forms are: Gain-scheduled control

Self – tuning

Model-reference adaptive systems

Gain – Scheduled Control:

With gain-scheduled control or, as it is sometimes referred to, pre-programmed adaptive control, pre-set changes in the parameters of the controller are made on the basis of some

auxiliary measurement of some process variable.

The term gain-scheduled control was used because the only parameter originally adjusted was gain

Self – Tuning:

With self-tuning control the system continuously tunes its own parameters based on monitoring the variable that the system is controlling and the output from the controller.

Self-tuning is often found in commercial PID controller, it generally then being referred to as auto-tuning.

When the operator presses a button, the controller injects a small disturbance into the system and measures the response.

Response is compared to the desired response and the control parameters adjusted, by modified Ziegler-Nichol rule, to bring the actual response closer to the desired response.

Model-Reference Adaptive Systems:

The model-reference system an accurate model of the system is developed.

The set value is then used as an input to both the actual and the model systems and the difference between the actual output and the output from the model compared. The difference in these signals is then used m adjusts the parameter of the controller to minimise the difference.