Syntax-Directed Translation Schemes

Syntax-Directed Translation Schemes

1 Postfix Translation Schemes

2 Parser-Stack Implementation of Postfix SDT's

3 SDT's With Actions Inside Productions

4 Eliminating Left Recursion From SDT's

5 SDT's for L-Attributed Definitions

6 Exercises for Section 5.4

Syntax-directed translation schemes are a complementary notation to syntax-directed definitions. All of the applications of syntax-directed definitions in Section 5.3 can be implemented using syntax-directed translation schemes.

From Section 2.3.5, a syntax-directed translation scheme (SDT) is a context-free grammar with program fragments embedded within production bodies. The program fragments are called semantic actions and can appear at any position within a production body. By convention, we place curly braces around actions; if braces are needed as grammar symbols, then we quote them.

Any SDT can be implemented by first building a parse tree and then per-forming the actions in a left-to-right depth-first order; that is, during a preorder traversal. An example appears in Section 5.4.3.

Typically, SDT's are implemented during parsing, without building a parse tree. In this section, we focus on the use of SDT's to implement two important classes of SDD's:

            The underlying grammar is LR-parsable, and the SDD is S-attributed.

            The underlying grammar is LL-parsable, and the SDD is L-attributed.

We shall see how, in both these cases, the semantic rules in an SDD can be converted into an SDT with actions that are executed at the right time. During parsing, an action in a production body is executed as soon as all the grammar symbols to the left of the action have been matched.

SDT's that can be implemented during parsing can be characterized by in-troducing distinct marker nonterminals in place of each embedded action; each marker M has only one production, M -» e. If the grammar with marker non-terminals can be parsed by a given method, then the SDT can be implemented during parsing.

1. Postfix Translation Schemes

By far the simplest SDD implementation occurs when we can parse the grammar bottom-up and the SDD is S-attributed. In that case, we can construct an SDT in which each action is placed at the end of the production and is executed along with the reduction of the body to the head of that production. SDT's with all actions at the right ends of the production bodies are called postfix SDT's.

Example 5.14 : The postfix SDT in Fig. 5.18 implements the desk calculator SDD of Fig. 5.1, with one change: the action for the first production prints a value. The remaining actions are exact counterparts of the semantic rules. Since the underlying grammar is LR, and the SDD is S-attributed, these actions can be correctly performed along with the reduction steps of the parser.

2. Parser-Stack Implementation of Postfix SDT's

Postfix SDT's can be implemented during LR parsing by executing the actions when reductions occur. The attribute(s) of each grammar symbol can be put on the stack in a place where they can be found during the reduction. The best plan is to place the attributes along with the grammar symbols (or the LR states that represent these symbols) in records on the stack itself.

In Fig. 5.19, the parser stack contains records with a field for a grammar symbol (or parser state) and, below it, a field for an attribute. The three grammar symbols X YZ are on top of the stack; perhaps they are about to be reduced according to a production like A —> X YZ. Here, we show X.x as the one attribute of X, and so on. In general, we can allow for more attributes, either by making the records large enough or by putting pointers to records on the stack. With small attributes, it may be simpler to make the records large enough, even if some fields go unused some of the time. However, if one or more attributes are of unbounded size — say, they are character strings — then it would be better to put a pointer to the attribute's value in the stack record and store the actual value in some larger, shared storage area that is not part of the stack.

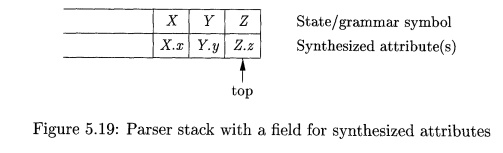
If the attributes are all synthesized, and the actions occur at the ends of the productions, then we can compute the attributes for the head when we reduce the body to the head. If we reduce by a production such as A X Y Z , then we have all the attributes of X, Y, and Z available, at known positions on the stack, as in Fig. 5.19. After the action, A and its attributes are at the top of the stack, in the position of the record for X.

Example 5.15 :  Let us rewrite the actions of the desk-calculator SDT of Ex ample 5.14 so that they manipulate the parser stack explicitly. Such stack manipulation is usually done automatically by the parser.

Suppose that the stack is kept in an array of records called stack, with top a cursor to the top of the stack. Thus, stack[top] refers to the top record on the stack, stack[top — 1] to the record below that, and so on. Also, we assume that each record has a field called val, which holds the attribute of whatever grammar symbol is represented in that record. Thus, we may refer to the attribute E.val that appears at the third position on the stack as stack[top — 2].val. The entire SDT is shown in Fig. 5.20.

For instance, in the second production, E -» E1 + T, we go two positions below the top to get the value of E±, and we find the value of T at the top. The resulting sum is placed where the head E will appear after the reduction, that is, two positions below the current top. The reason is that after the reduction, the three topmost stack symbols are replaced by one. After computing E.val, we pop two symbols off the top of the stack, so the record where we placed E.val will now be at the top of the stack.

In the third production, E —> T, no action is necessary, because the length of the stack does not change, and the value of T.val at the stack top will simply become the value of E.val.  The same observation applies to the productions T ->• F and F digit .  Production F ->• ( E) is slightly different.  Although the value does not change, two positions are removed from the stack during the reduction, so the value has to move to the position after the reduction.

Note that we have omitted the steps that manipulate the first field of the stack records — the field that gives the LR state or otherwise represents the grammar symbol. If we are performing an LR parse, the parsing table tells us what the new state is every time we reduce; see Algorithm 4.44. Thus, we may simply place that state in the record for the new top of stack.

3. SDT's With Actions Inside Productions

An action may be placed at any position within the body of a production.

It is performed immediately after all symbols to its left are processed. Thus,

if we have a production B -» X {a} Y, the action a is done after we have recognized X (if X is a terminal) or all the terminals derived from X (if X is a nonterminal). More precisely,

• If the parse is bottom-up, then we perform action a as soon as this oc-currence of X appears on the top of the parsing stack.

• If the parse is top-down, we perform a just before we attempt to expand this occurrence of Y (if Y a nonterminal) or check for Y on the input (if Y is a terminal).

SDT's that can be implemented during parsing include postfix SDT's and a class of SDT's considered in Section 5.5 that implements L-attributed defini-tions. Not all SDT's can be implemented during parsing, as we shall see in the next example.

Example 5.16 : As an extreme example of a problematic SDT, suppose that we turn our desk-calculator running example into an SDT that prints the prefix form of an expression, rather than evaluating the expression. The productions and actions are shown in Fig. 5.21.

Unfortunately, it is impossible to implement this SDT during either top-down or bottom-up parsing, because the parser would have to perform critical actions, like printing instances of * or +, long before it knows whether these symbols will appear in its input.

Using marker nonterminals M2 and M4 for the actions in productions 2 and 4, respectively, on input 3, a shift-reduce parser (see Section 4.5.3) has conflicts between reducing by M2 -> e, reducing by M4 —> e, and shifting the digit.

Any SDT can be implemented as follows:

 Ignoring the actions, parse the input and produce a parse tree as a result.

 Then, examine each interior node N, say one for production A -± a.  Add additional children to N for the actions in a,  so the children of N from left to right have exactly the symbols and actions of a. 

 3. Perform a preorder traversal (see Section 2.3.4)  of the tree, and as soon as a node labeled by an action is visited, perform that action.

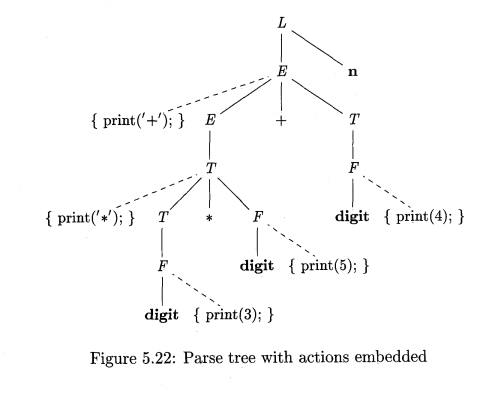
 For instance,  Fig.  5.22 shows the parse tree for expression 3 * 5 + 4 with actions inserted. If we visit the nodes in preorder, we get the prefix form of the expression: + * 3 5 4.

4. Eliminating Left Recursion From SDT's

Since no grammar with left recursion can be parsed deterministically top-down, we examined left-recursion elimination in Section 4.3.3. When the grammar is part of an SDT, we also need to worry about how the actions are handled.

First, consider the simple case, in which the only thing we care about is the order in which the actions in an SDT are performed. For example, if each action simply prints a string, we care only about the order in which the strings are printed. In this case, the following principle can guide us:

When transforming the grammar, treat the actions as if they were termi-nal symbols.

This principle is based on the idea that the grammar transformation preserves the order of the terminals in the generated string. The actions are therefore executed in the same order in any left-to-right parse, top-down or bottom-up.

The  "trick" for eliminating left recursion is to take two productions

A -> Aaa | b

that generate strings consisting of a j3 and any number of en's, and replace them by productions that generate the same strings using a new nonterminal R (for "remainder") of the first production:

A->bR

R —»• aR | e

If (3 does not begin with A, then A no longer has a left-recursive production. In regular-definition terms, with both sets of productions, A is defined by 0(a)*. See Section 4.3.3 for the handling of situations where A has more recursive or nonrecursive productions.

Exampl e 5 . 1 7 : Consider the following E-productions from an SDT for trans-lating infix expressions into postfix notation:

E       ->      E i + T   { print('+'); }

E       ->      T

If we apply the standard transformation to E, the remainder of the left-recursive production is

          a        =       +  T { print('-r'); }

and    the body of the other production is T.  If we introduce R for the remain-

der of E, we get the set of productions:

          E        -->         T  R

          R       -->      + T { printC-h'); } R

          R       ->     e

When the actions of an SDD compute attributes rather than merely printing output, we must be more careful about how we eliminate left recursion from a grammar. However, if the SDD is S-attributed, then we can always construct an SDT by placing attribute-computing actions at appropriate positions in the new productions.

We shall give a general schema for the case of a single recursive production, a single nonrecursive production, and a single attribute of the left-recursive nonterminal; the generalization to many productions of each type is not hard, but is notationally cumbersome. Suppose that the two productions are A 

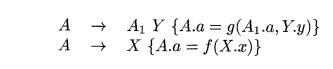
Here, X.a is the synthesized attribute of left-recursive nonterminal A, and X and Y are single grammar symbols with synthesized attributes X.x and Y.y, respectively. These could represent a string of several grammar symbols, each with its own attribute(s), since the schema has an arbitrary function g computing A.a in the recursive production and an arbitrary function / computing A.a in the second production. In each case, / and g take as arguments whatever attributes they are allowed to access if the SDD is S-attributed.

We want to turn the underlying grammar into

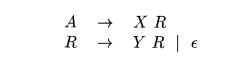
Figure 5.23 suggests what the SDT on the new grammar must do. In (a) we see the effect of the postfix SDT on the original grammar. We apply / once, corresponding to the use of production A -> X, and then apply g as many times as we use the production A AY. Since R generates a "remainder" of Y's, its translation depends on the string to its left, a string of the form XYY • • Y. Each use of the production R -> YR results in an application of g. For R, we use an inherited attribute R.i to accumulate the result of successively applying g, starting with the value of A.a.

In addition, R has a synthesized attribute R.s, not shown in Fig. 5.23.

This attribute is first computed when R ends its generation of Y symbols, as signaled by the use of production R —>• e. R.s is then copied up the tree, so it can become the value of A.a for the entire expression XYY • • • Y. The case where A generates XYY is shown in Fig. 5.23, and we see that the value of A.a at the root of (a) has two uses of g. So does R.i at the bottom of tree (b), and it is this value of R.s that gets copied up that tree.

To accomplish this translation, we use the following SDT:

Notice that the inherited attribute R.i is evaluated immediately before a use of R in the body, while the synthesized attributes A.a and -R.s are evaluated at the ends of the productions. Thus, whatever values are needed to compute these attributes will be available from what has been computed to the left.

3. SDT's for L-Attributed Definitions

In Section 5.4.1, we converted S-attributed SDD's into postfix SDT's, with actions at the right ends of productions. As long as the underlying grammar is LR, postfix SDT's can be parsed and translated bottom-up.

Now, we consider the more general case of an L-attributed SDD. We shall assume that the underlying grammar can be parsed top-down, for if not it is frequently impossible to perform the translation in connection with either an LL or an LR parser. With any grammar, the technique below can be imple-mented by attaching actions to a parse tree and executing them during preorder traversal of the tree.

The rules for turning an L-attributed SDD into an SDT are as follows:

1. Embed the action that computes the inherited attributes for a nonterminal A immediately before that occurrence of A in the body of the production. If several inherited attributes for A depend on one another in an acyclic fashion, order the evaluation of attributes so that those needed first are computed first.

            Place the actions that compute a synthesized attribute for the head of a production at the end of the body of that production.

We shall illustrate these principles with two extended examples. The first involves typesetting. It illustrates how the techniques of compiling can be used in language processing for applications other than what we normally think of as programming languages. The second example is about the generation of intermediate code for a typical programming-language construct: a form of while-statement.

E x a m p l e 5 . 1 8 : This example is motivated by languages for typesetting math - ematical formulas. Eqn is an early example of such a language; ideas from Eqn are still found in the TEX typesetting system, which was used to produce this book.

We shall concentrate on only the capability to define subscripts, subscripts of subscripts, and so on, ignoring superscripts, built-up fractions, and all other mathematical features. In the Eqn language, one writes a sub i sub j to set the expression aij. A simple grammar for boxes (elements of text bounded by a rectangle) is

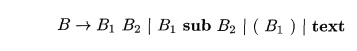
Corresponding to these four productions, a box can be either         

1.       Two boxes, juxtaposed, with  the     first,  B1, to the    left of the other, B2.

2. A box and a subscript box. The second box appears in a smaller size, lower, and to the right of the first box.

3. A parenthesized box, for grouping of boxes and subscripts. Eqn and I g X both use curly braces for grouping, but we shall use ordinary, round paren-theses to avoid confusion with the braces that surround actions in SDT's.

4. A text string, that is, any string of characters.

This grammar is ambiguous, but we can still use it to parse bottom-up if we make subscripting and juxtaposition right associative, with s u b taking precedence over juxtaposition.

Expressions will be typeset by constructing larger boxes out of smaller ones.

In Fig. 5.24, the boxes for E1 and .height are about to be juxtaposed to form the box for Ei.height. The left box for E1 is itself constructed from the box for E and the subscript 1. The subscript 1 is handled by shrinking its box by about 30%, lowering it, and placing it after the box for E. Although we shall treat .height as a text string, the rectangles within its box show how it can be constructed from boxes for the individual letters.

In this example, we concentrate on the vertical geometry of boxes only. The horizontal geometry — the widths of boxes — is also interesting, especially when different characters have different widths. It may not be readily apparent, but each of the distinct characters in Fig. 5.24 has a different width.

The values associated with the vertical geometry of boxes are as follows:

a)                 The point size is used to set text within a box. We shall assume that characters not in subscripts are set in 10 point type, the size of type in this book. Further, we assume that if a box has point size p, then its subscript box has the smaller point size 0.7p. Inherited attribute B.ps will represent the point size of block B. This attribute must be inherited, because the context determines by how much a given box needs to be shrunk, due to the number of levels of subscripting.

b)        Each box has a baseline, which is a vertical position that corresponds to the bottoms of lines of text, not counting any letters, like "g" that extend below the normal baseline. In Fig. 5.24, the dotted line represents the baseline for the boxes E, .height, and the entire expression. The baseline

for the box containing the subscript 1 is adjusted to lower the subscript.

c)          A box has a height, which is the distance from the top of the box to the baseline. Synthesized attribute B.ht gives the height of box B.

d)         A box has a depth, which is the distance from the baseline to the bottom of the box. Synthesized attribute B.dp gives the depth of box B.

The SDD in Fig. 5.25 gives rules for computing point sizes, heights, and depths. Production 1 is used to assign B.ps the initial value 10.

Production 2 handles juxtaposition. Point sizes are copied down the parse tree; that is, two sub-boxes of a box inherit the same point size from the larger box. Heights and depths are computed up the tree by taking the maximum. That is, the height of the larger box is the maximum of the heights of its two components, and similarly for the depth.

Production 3 handles subscripting and is the most subtle. In this greatly simplified example, we assume that the point size of a subscripted box is 70% of the point size of its parent. Reality is much more complex, since subscripts cannot shrink indefinitely; in practice, after a few levels, the sizes of subscripts shrink hardly at all. Further, we assume that the baseline of a subscript box drops by 25% of the parent's point size; again, reality is more complex.

Production 4 copies attributes appropriately when parentheses are used. Fi-nally, production 5 handles the leaves that represent text boxes. In this matter too, the true situation is complicated, so we merely show two unspecified func-tions getHt and getDp that examine tables created with each font to determine the maximum height and maximum depth of any characters in the text string. The string itself is presumed to be provided as the attribute lexval of terminal t e x t .

Our last task is to turn this SDD into an SDT, following the rules for an L-attributed SDD, which Fig. 5.25 is. The appropriate SDT is shown in Fig. 5.26. For readability, since production bodies become long, we split them across lines and line up the actions. Production bodies therefore consist of the contents of all lines up to the head of the next production.

Our next example concentrates on a simple while-statement and the gener-ation of intermediate code for this type of statement. Intermediate code will be treated as a string-valued attribute. Later, we shall explore techniques that involve the writing of pieces of a string-valued attribute as we parse, thus avoid-ing the copying of long strings to build even longer strings. The technique was introduced in Example 5.17, where we generated the postfix form of an infix expression "on-the-fly," rather than computing it as an attribute. However, in our first formulation, we create a string-valued attribute by concatenation.

E x a m p l e 5 . 1 9 :  For this example, we only need one production:

S -> while ( C ) Si

Here, S is the nonterminal that generates all kinds of statements, presumably including if-statements, assignment statements, and others. In this example, C stands for a conditional expression — a boolean expression that evaluates to true or false.

In this flow-of-control example, the only things we ever generate are labels. All the other intermediate-code instructions are assumed to be generated by parts of the SDT that are not shown. Specifically, we generate explicit instruc-tions of the form l a b e l L, where L is an identifier, to indicate that L is the label of the instruction that follows. We assume that the intermediate code is like that introduced in Section 2.8.4.

The meaning of our while-statement is that the conditional C is evaluated. If it is true, control goes to the beginning of the code for Si. If false, then control goes to the code that follows the while-statement's code. The code for Si must be designed to jump to the beginning of the code for the while-statement when finished; the jump to the beginning of the code that evaluates C is not shown in Fig. 5.27.

We use the following attributes to generate the proper intermediate code:

1. The inherited attribute S.next labels the beginning of the code that must be executed after S is finished.

2. The synthesized attribute S.code steps s the sequence of intermediate-code S and that implements a statement ends with a jump to S.next.

3. The inherited attribute C.true labels the beginning of the code that must be executed if C is true.

4. The inherited attribute C.false labels the beginning of the code that must be executed if C is false.

 The synthesized attribute C.code is the sequence of intermediate-code steps that implements the condition C and jumps either to C.true or to C.false, depending on whether C is true or false.

The SDD that computes these attributes for the while-statement is shown in Fig. 5.27. A number of points merit explanation:

• The function new generates new labels.

 The variables LI and L2 hold labels that we need in the code. LI is the beginning of the code for the while-statement, and we need to arrange

 Figure 5.27: SDD for while-statements that Si jumps there after it finishes. That is why we set Si.next to LI.

 L2 is the beginning of the code for Si, and it becomes the value of C.true, because we branch there when C is true.

• Notice that C.false is set to S.next, because when the condition is false, we execute whatever code must follow the code for S.

 We use || as the symbol for concatenation of intermediate-code fragments. The value of S.code thus begins with the label LI, then the code for condition C, another label L2, and the code for Si.

This SDD is L-attributed. When we convert it into an SDT, the only re-maining issue is how to handle the labels LI and L2, which are variables, and not attributes. If we treat actions as dummy nonterminals, then such variables can be treated as the synthesized attributes of dummy nonterminals. Since LI and L2 do not depend on any other attributes, they can be assigned to the first action in the production. The resulting SDT with embedded actions that implements this L-attributed definition is shown in Fig. 5.28.

6. Exercises for Section 5.4

Exercise 5 . 4 . 1 : We mentioned in Section 5.4.2 that it is possible to deduce, from the LR state on the parsing stack, what grammar symbol is represented by the state. How would we discover this information?

Exercise 5 . 4 . 2:  Rewrite the following SDT:                       

A       A {a} B | A B {b}          |         0

B ->   B {c} A | B A       {d}    |         1

so that the underlying grammar becomes non-left-recursive. Here, a, 6, c, and d are actions, and 0 and 1 are terminals.

! Exercise 5 . 4 . 3 : The following SDT computes the value of a string of O's and l's interpreted as a positive, binary integer.

B       -»      Br      0  {B.val     = 2 x Bx.val]

          |         Bx     1  {B.val     = 2 x Bx.val + 1}

          j         1        {B.val = 1}

Rewrite this SDT so the underlying grammar is not left recursive, and yet the same value of B.val is computed for the entire input string.

! Exercise 5 . 4 . 4: Write L-attributed SDD's analogous to that of Example 5.19 for the following productions, each of which represents a familiar flow-of-control construct, as in the programming language C. You may need to generate a three-address statement to jump to a particular label L, in which case you should generate goto L.

a)       S       -)• if ( C )     Si else S2   

b)      S       do Si while ( C )  

c)       S       -4'{' L         '}';     L       L S    1  e

Note that any statement in the list can have a jump from its middle to the next Statement, so it is not sufficient simply to generate code for each statement in order.

Exercise 5 . 4 . 5 : Convert each of your SDD's from Exercise 5.4.4 to an SDT in the manner of Example 5.19.

Exercise 5 . 4 . 6 : Modify the SDD of Fig. 5.25 to include a synthesized attribute B.le, the length of a box. The length of the concatenation of two boxes is the sum of the lengths of each. Then add your new rules to the proper positions in the SDT of Fig. 5.26

Exercise 5 . 4 . 7: Modify the SDD of Fig. 5.25 to include superscripts denoted by operator sup between boxes. If box B₂ is a superscript of box Bi, then position the baseline of B₂ 0.6 times the point size of Bi above the baseline of Bi. Add the new production and rules to the SDT of Fig. 5.26.