Applications of Syntax-Directed Translation

Applications of Syntax-Directed Translation

1 Construction of Syntax Trees

2 The Structure of a Type

3 Exercises for Section 5.3

The syntax-directed translation techniques in this chapter will be applied in Chapter 6 to type checking and intermediate-code generation. Here, we consider selected examples to illustrate some representative SDD's.

The main application in this section is the construction of syntax trees. Since some compilers use syntax trees as an intermediate representation, a common form of SDD turns its input string into a tree. To complete the translation to intermediate code, the compiler may then walk the syntax tree, using another set of rules that are in effect an SDD on the syntax tree rather than the parse tree. (Chapter 6 also discusses approaches to intermediate-code generation that apply an SDD without ever constructing a tree explicitly.)

We consider two SDD's for constructing syntax trees for expressions. The first, an S-attributed definition, is suitable for use during bottom-up parsing. The second, L-attributed, is suitable for use during top-down parsing.

The final example of this section is an L-attributed definition that deals with basic and array types.

1. Construction of Syntax Trees

As discussed in Section 2.8.2, each node in a syntax tree represents a construct; the children of the node represent the meaningful components of the construct. A syntax-tree node representing an expression E1 + E₂ has label + and two children representing the subexpressions E1 and E₂ •

We shall implement the nodes of a syntax tree by objects with a suitable number of fields. Each object will have an op field that is the label of the node.

The objects will have additional fields as follows:

• If the node is a leaf, an additional field holds the lexical value for the leaf. A constructor function Leaf (op, val) creates a leaf object. Alternatively, if nodes are viewed as records, then Leaf returns a pointer to a new record for a leaf.

• If the node is an interior node, there are as many additional fields as the node has children in the syntax tree. A constructor function Node takes two or more arguments: Node(op,ci,c2,... ,ck) creates an object with first field op and k additional fields for the k children c1,... , .

Example 5.11 : The S-attributed definition in Fig. 5.10 constructs syntax trees for a simple expression grammar involving only the binary operators + and -. As usual, these operators are at the same precedence level and are jointly left associative. All nonterminals have one synthesized attribute node, which represents a node of the syntax tree.

Every time the first production E E1 + T is used, its rule creates a node with ' + ' for op and two children, Ei.node and T.node, for the subexpressions.

The second production has a similar rule.

For production 3, E -> T, no node is created, since E.node is the same as T.node. Similarly, no node is created for production 4, T ( E ) . The value of T.node is the same as E.node, since parentheses are used only for grouping; they influence the structure of the parse tree and the syntax tree, but once their job is done, there is no further need to retain them in the syntax tree.

The last two T-productions have a single terminal on the right. We use the constructor Leaf to create a suitable node, which becomes the value of T.node.

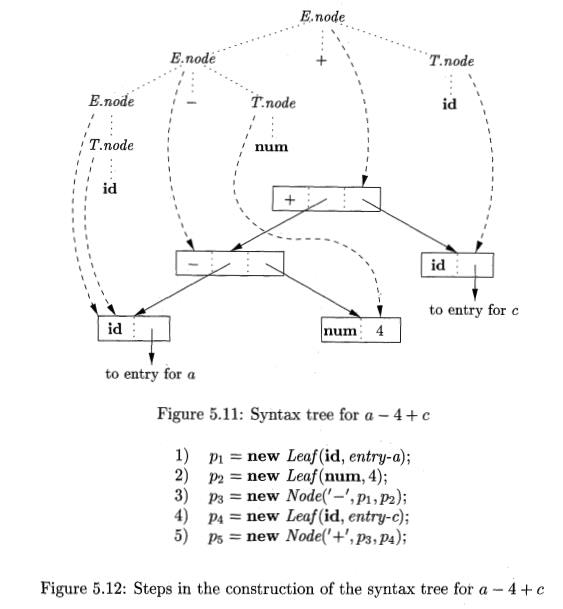
Figure 5 . 1 1 shows the construction of a syntax tree for the input a — 4 + c. The nodes of the syntax tree are shown as records, with the op field first. Syntax-tree edges are now shown as solid lines. The underlying parse tree, which need not actually be constructed, is shown with dotted edges. The third type of line, shown dashed, represents the values of E.node and T-node; each line points to the appropriate syntax-tree node.

At the bottom we see leaves for a, 4 and c, constructed by Leaf. We suppose that the lexical value id. entry points into the symbol table, and the lexical value uum.ual is the numerical value of a constant. These leaves, or pointers to them, become the value of T.node at the three parse-tree nodes labeled T, according to rules 5 and 6. Note that by rule 3, the pointer to the leaf for a is also the value of E.node for the leftmost E in the parse tree.

Rule 2 causes us to create a node with op equal to the minus sign and pointers to the first two leaves. Then, rule 1 produces the root node of the syntax tree by combining the node for — with the third leaf.

If the rules are evaluated during a postorder traversal of the parse tree, or with reductions during a bpttom-up parse, then the sequence of steps shown in Fig. 5 . 1 2 ends with p5 pointing to the root of the constructed syntax tree. •

With a grammar designed for top-down parsing, the same syntax trees are constructed, using the same sequence of steps, even though the structure of the parse trees differs significantly from that of syntax trees.

Example 5.12 : The L-attributed definition in Fig. 5 . 1 3 performs the same translation as the S-attributed definition in Fig. 5 . 1 0 . The attributes for the grammar symbols E, T, id, and n u m are as discussed in Example 5 . 1 1 .

The rules for building syntax trees in this example are similar to the rules for the desk calculator in Example 5.3.  In the desk-calculator         example, a term x * y  was evaluated by passing x  as an inherited attribute,  since x  and  * y appeared in different portions of the parse tree. Here, the idea is to build a syntax tree for x + y by passing x as an inherited attribute, since x and + y appear in different subtrees. Nonterminal E' is the counterpart of nonterminal T" in Example 5.3. Compare the dependency graph for a — 4 + c in Fig. 5.14 with that for 3 * 5 in Fig. 5.7.

Nonterminal E' has an inherited attribute iinh and a synthesized attribute syn. Attribute E'.inh represents the partial syntax tree constructed so far. Specifically, it represents the root of the tree for the prefix of the input string that is to the left of the subtree for E'. At node 5 in the dependency graph in Fig. 5.14, E'.inh denotes the root of the partial syntax tree for the identifier a; that is, the leaf for a. At node 6, E'.inh denotes the root for the partial syntax

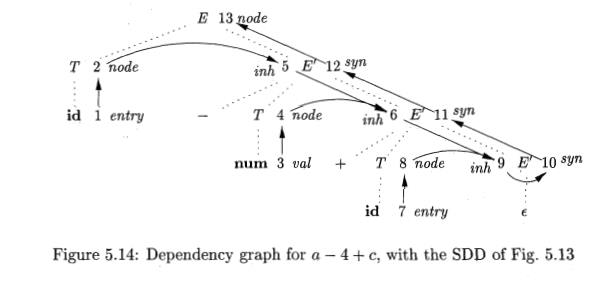
tree for the input a — 4. At node 9, E'.inh denotes the syntax tree for a — 4 + c. Since there is no more input, at node 9, E'.inh points to the root of the entire syntax tree. The syn attributes pass this value back up the parse tree until it becomes the value of E.node. Specifically, the attribute value at node 10 is defined by the rule E'.syn = E'.inh associated with the production E' —> e.

The attribute value at node 11 is defined by the rule E'.syn = E[ .syn associated with production 2 in Fig. 5 . 1 3 . Similar rules define the attribute values at nodes 12 and 1 3 .

2. The Structure of a Type

Inherited attributes are useful when the structure of the parse tree differs from the abstract syntax of the input; attributes can then be used to carry information from one part of the parse tree to another. The next example shows how a mismatch in structure can be due to the design of the language, and not due to constraints imposed by the parsing method.

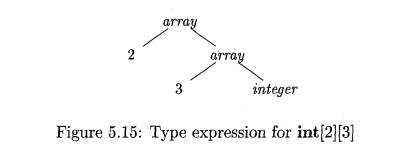
Example 5.13 : In C, the type int [2][3] can be read as, "array of 2 arrays of 3 integers." The corresponding type expression array(2, array(3, integer)) is represented by the tree in Fig. 5.15. The operator array takes two parameters, a number and a type. If types are represented by trees, then this operator returns a tree node labeled array with two children for a number and a type.

With the SDD in Fig. 5.16, nonterminal T generates either a basic type or an array type. Nonterminal B generates one of the basic types int and float. T generates a basic type when T derives B C and C derives e. Otherwise, C generates array components consisting of a sequence of integers, each integer surrounded by brackets.

The nonterminals B and T have a synthesized attribute t representing a type. The nonterminal C has two attributes: an inherited attribute b and a synthesized attribute t. The inherited b attributes pass a basic type down the tree, and the synthesized t attributes accumulate the result.

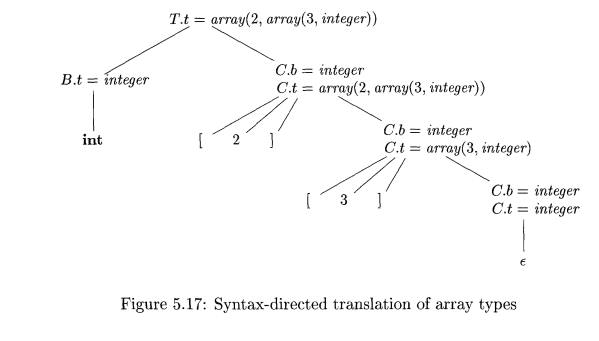
An annotated parse tree for the input string int [ 2 ] [ 3 ] is shown in Fig. 5.17. The corresponding type expression in Fig. 5.15 is constructed by passing the type integer from B, down the chain of C's through the inherited attributes b. The array type is synthesized up the chain of C's through the attributes t.

In more detail, at the root for T -» B C, nonterminal C inherits the type from B, using the inherited attribute C.b. At the rightmost node for C, the production is C e, so C.t equals C.6.  The semantic rules for the production C [ num ] C1 form C.t by applying the operator array to the operands num.ua/ and C1.t.

3. Exercises for Section 5.3

Exercise 5 . 3 . 1 : Below is a grammar for expressions involving operator 4- and integer or floating-point operands. Floating-point numbers are distinguished by having a decimal point.

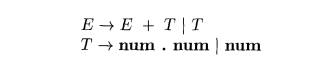
            Give an SDD to determine the type of each term T and expression E.

            Extend your SDD of (a) to translate expressions into postfix notation. Use the unary operator intToFloat to turn an integer into an equivalent float.

Exercise 5.3.2 : Give an SDD to translate infix expressions with + and * into equivalent expressions without redundant parentheses. For example, since both operators associate from the left, and * takes precedence over +, ((a*(6+c))*(<i)) translates into a * (b + c) * d.

Exercise 5 . 3 . 3 : Give an SDD to differentiate expressions such as x * (3 * x + x * x) involving the operators + and *, the variable x, and constants. Assume that no simplification occurs, so that, for example, 3 * x will be translated into 3 * 1 + 0 * x.