Syntax-Directed Definitions

Syntax-Directed Definitions

1 Inherited and Synthesized Attributes

2 Evaluating an SDD at the Nodes of a Parse Tree

3 Exercises for Section 5.1

A syntax-directed definition (SDD) is a context-free grammar together with attributes and rules. Attributes are associated with grammar symbols and rules are associated with productions. If X is a symbol and a is one of its attributes, then we write X.a to denote the value of a at a particular parse-tree node labeled X. If we implement the nodes of the parse tree by records or objects, then the attributes of X can be implemented by data fields in the records that represent the nodes for X. Attributes may be of any kind: numbers, types, table references, or strings, for instance. The strings may even be long sequences of code, say code in the intermediate language used by a compiler.

1. Inherited and Synthesized Attributes

We shall deal with two kinds of attributes for nonterminals:

1. A synthesized attribute for a nonterminal A at a parse-tree node N is defined by a semantic rule associated with the production at N. Note that the production must have A as its head. A synthesized attribute at node N is defined only in terms of attribute values at the children of N and at N itself.

2. An inherited attribute for a nonterminal B at a parse-tree node N is defined by a semantic rule associated with the production at the parent of N. Note that the production must have B as a symbol in its body. An inherited attribute at node N is defined only in terms of attribute values at JV's parent, N itself, and N's siblings.

An Alternative Definition of Inherited Attributes

No additional translations are enabled if we allow an inherited attribute B.c at a node N to be defined in terms of attribute values at the children of A?", as well as at N itself, at its parent, and at its siblings. Such rules can be "simulated" by creating additional attributes of B, say B.ci,B.c2,....

These are synthesized attributes that copy the needed attributes of the children of the node labeled B. We then compute B.c as an inherited attribute, using the attributes B.ci, B.c2,... in place of attributes at the children. Such attributes are rarely needed in practice.

While we do not allow an inherited attribute at node N to be defined in terms of attribute values at the children of node N, we do allow a synthesized attribute at node N to be defined in terms of inherited attribute values at node N itself.

Terminals can have synthesized attributes, but not inherited attributes. At-tributes for terminals have lexical values that are supplied by the lexical analyzer; there are ho semantic rules in the SDD itself for computing the value of an attribute for a terminal.

Example 5.1 : The SDD in Fig. 5 . 1 is based on our familiar grammar for arithmetic expressions with operators + and *. It evaluates expressions termi-nated by an endmarker n. In the SDD, each of the nonterminals has a single synthesized attribute, called val We also suppose that the terminal digit has a synthesized attribute lexval, which is an integer value returned by the lexical analyzer.

The rule for production 1, L ->• E n, sets L.val to E.val, which we shall see is the numerical value of the entire expression.

Production 2, E -> Ex + T, also has one rule, which computes the val attribute for the head E as the sum of the values at E1 and T. At any parse tree node N labeled E, the value of val for E is the sum of the values of val at the children of node N labeled E and T.

Production 3, E -»• T, has a single rule that defines the value of val for E to be the same as the value of val at the child for T. Production 4 is similar to the second production; its rule multiplies the values at the children instead of adding them. The rules for productions 5 and 6 copy values at a child, like that for the third production. Production 7 gives F.val the value of a digit, that is, the numerical value of the token digit that the lexical analyzer returned.

An SDD that involves only synthesized attributes is called S-attributed; the SDD in Fig. 5.1 has this property. In an S-attributed SDD, each rule computes an attribute for the nonterminal at the head of a production from attributes taken from the body of the production.

For simplicity, the examples in this section have semantic rules without side effects. In practice, it is convenient to allow SDD's to have limited side effects, such as printing the result computed by a desk calculator or interacting with a symbol table. Once the order of evaluation of attributes is discussed in Section 5.2, we shall allow semantic rules to compute arbitrary functions, possibly involving side effects.

An S-attributed SDD can be implemented naturally in conjunction with an LR parser. In fact, the SDD in Fig. 5.1 mirrors the Yacc program of Fig. 4.58, which illustrates translation during LR parsing. The difference is that, in the rule for production 1, the Yacc program prints the value E.val as a side effect, instead of defining the attribute L.val.

An SDD without side effects is sometimes called an attribute grammar. The rules in an attribute grammar define the value of an attribute purely in terms of the values of other attributes and constants.

2. Evaluating an SDD at the Nodes of a Parse Tree

To visualize the translation specified by an SDD, it helps to work with parse trees, even though a translator need not actually build a parse tree. Imagine therefore that the rules of an SDD are applied by first constructing a parse tree and then using the rules to evaluate all of the attributes at each of the nodes of the parse tree.  A parse tree, showing the value(s) of its attribute(s) is called an annotated  parse  tree.

How do we construct an annotated parse tree? In what order do we evaluate attributes? Before we can evaluate an attribute at a node of a parse tree, we must evaluate all the attributes upon which its value depends. For example, if all attributes are synthesized, as in Example 5.1, then we must evaluate the val attributes at all of the children of a node before we can evaluate the val attribute at the node itself.

With synthesized attributes, we can evaluate attributes in any bottom-up order, such as that of a postorder traversal of the parse tree; the evaluation of S-attributed definitions is discussed in Section 5.2.3.

For SDD's with both inherited and synthesized attributes, there is no guar-antee that there is even one order in which to evaluate attributes at nodes. For instance, consider nonterminals A and B, with synthesized and inherited attributes A.s and BA, respectively, along with the production and rules

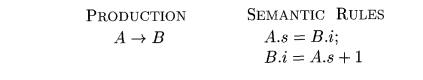
These rules are circular; it is impossible to evaluate either A.s at a node N or BA at the child of N without first evaluating the other. The circular dependency of A.s and BA at some pair of nodes in a parse tree is suggested by Fig. 5.2.

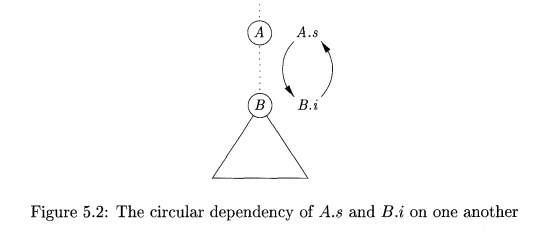
Figure 5.2:  The circular dependency of A.s and BA on one another

It is computationally difficult to determine whether or not there exist any circularities in any of the parse trees that a given SDD could have to translate.¹ Fortunately, there are useful subclasses of SDD's that are sufficient to guarantee that an order of evaluation exists, as we shall see in Section 5.2.

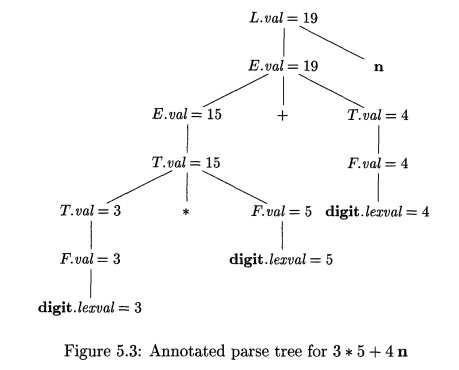
Example 5.2 : Figure 5.3 shows an annotated parse tree for the input string 3 * 5 + 4 n, constructed using the grammar and rules of Fig. 5.1. The values of lexval are presumed supplied by the lexical analyzer. Each of the nodes for the nonterminals has attribute val computed in a bottom-up order, and we see the resulting values associated with each node. For instance, at the node with a child labeled *, after computing T.val = 3 and F.val = 5 at its first and third children, we apply the rule that says T.val is the product of these two values, or 15.

Inherited attributes are useful when the structure of a parse tree does not "match" the abstract syntax of the source code. The next example shows how inherited attributes can be used to overcome such a mismatch due to a grammar designed for parsing rather than translation.

1 Without going into details, while the problem is decidable, it cannot be solved by a polynomial-time algorithm, even if V = NT, since it has exponential time complexity.

Example 5.3 : The SDD in Fig. 5.4 computes terms like 3 * 5 and 3 * 5 * 7 .

The top-down parse of input 3 * 5 begins with the production T ^ FT'. Here, F generates the digit 3, but the operator * is generated by X". Thus, the left operand 3 appears in a different subtree of the parse tree from *. An inherited attribute will therefore be used to pass the operand to the operator.

The grammar in this example is an excerpt from a non-left-recursive version of the familiar expression grammar; we used such a grammar as a running example to illustrate top-down parsing in Section 4.4.

Figure 5.4:  An SDD based on a grammar suitable for top-down parsing

Each of the nonterminals T and F has a synthesized attribute val; the terminal digit has a synthesized attribute lexval. The nonterminal T has two attributes: an inherited attribute inh and a synthesized attribute syn.

The semantic rules are based on the idea that the left operand of the operator * is inherited. More precisely, the head T" of the production T' * F T[ inherits the left operand of * in the production body. Given a term x * y * z, the root of the subtree for * y * z inherits x. Then, the root of the subtree for * z inherits the value of x * y, and so on, if there are more factors in the term.

Once all the factors have been accumulated, the result is passed back up the tree using synthesized attributes.

To see how the semantic rules are used, consider the annotated parse tree for 3 * 5 in Fig. 5.5. The leftmost leaf in the parse tree, labeled digit, has attribute value lexval = 3, where the 3 is supplied by the lexical analyzer. Its parent is for production 4, F -> digit. The only semantic rule associated with this production defines F.val = digit.lexval, which equals 3.

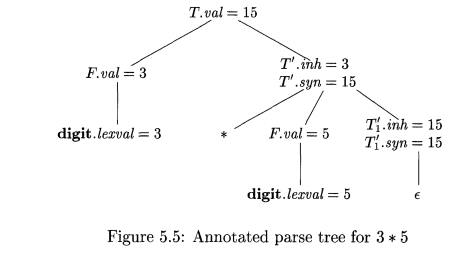
At the second child of the root, the inherited attribute T'.inh is defined by the semantic rule T'.inh = F.val associated with production 1. Thus, the left operand, 3, for the * operator is passed from left to right across the children of the root.

The production at the node for V is X" -»• * FT[. (We retain the subscript 1 in the annotated parse tree to distinguish between the two nodes for T'.) The inherited attribute T[.inh is defined by the semantic rule T[.inh = T'.inhx F.val associated with production 2.

With  T'.inh  =  3  and   F.val =        5,       we     get  T[.inh   = 1 5 .  At   the  lower node for T[,  the production is     T"  ->•        e.       The    semantic     rule T'.syn  —  T'.inh defines T{.syn — 15. The syn attributes at the nodes for X" pass the value 15 up the tree to the node for X, where T.val = 15.

3. Exercises for Section 5.1

Exercise 5.1.1 : For the SDD of Fig. 5.1, give annotated parse trees for the following expressions:

a)       (3 + 4 ) * ( 5 + 6 ) n .

            1 * 2 * 3 * (4 + 5) n.

            (9 + 8 * (7 + 6 ) + 5) * 4 n .

E x e r c i s e 5 . 1 . 2: Extend the SDD of Fig. 5.4 to handle expressions as in Fig. 5.1.

E x e r c i s e 5 . 1 . 3 :  Repeat Exercise 5.1.1, using your SDD from Exercise 5.1.2.