Chapter: Compilers : Principles, Techniques, & Tools : Syntax-Directed Translation
Evaluation Orders for SDD's
Evaluation Orders for SDD's
1 Dependency Graphs
2 Ordering the Evaluation of
Attributes
3 S-Attributed Definitions
4 L-Attributed Definitions
5 Semantic Rules with Controlled
Side Effects
6 Exercises for Section 5.2
"Dependency graphs" are a useful tool for determining an
evaluation order for the attribute instances in a given parse tree. While an
annotated parse tree shows the values of attributes, a dependency graph helps
us determine how those values can be computed.
In this section, in addition to dependency graphs, we define two
impor-tant classes of SDD's: the "S-attributed" and the more general
"L-attributed" SDD's. The translations specified by these two classes
fit well with the parsing methods we have studied, and most translations
encountered in practice can be written to conform to the requirements of at
least one of these classes.
1. Dependency Graphs
A dependency graph depicts the
flow of information among the attribute in-stances in a particular parse tree;
an edge from one attribute instance to an-other means that the value of the
first is needed to compute the second. Edges express constraints implied by the
semantic rules. In more detail:
For each parse-tree node, say a
node labeled by grammar symbol X, the
dependency graph has a node for each attribute associated with X.
Suppose that a semantic rule
associated with a production p
defines the value of synthesized attribute A.b
in terms of the value of X.c (the
rule
may define A.b in terms of
other attributes in addition to X.c).
Then, the dependency graph has an edge from X.c
to A.b. More precisely, at every node
N labeled A where production p is
applied, create an edge to attribute b
at N, from the attribute c at the
child of N corresponding to this
instance of the symbol X in the body
of the production.2
Suppose that a semantic rule
associated with a production p
defines the value of inherited attribute B.c
in terms of the value of X.a. Then,
the dependency graph has an edge from X.a
to B.c. For each node N labeled B that corresponds to an occurrence of this B in the body of production
p, create an edge to attribute c at N
from the attribute a at the node M that corresponds to this occurrence
of X. Note that M could be either the parent or a sibling of N.
Since a
node N
can have several children labeled X, we again assume that subscripts
distinguish among uses of the same symbol at different places in the
production.
Example
5.4: Consider the following production and rule:

At every node N labeled E, with children corresponding to the
body of this production, the synthesized attribute val at N is computed
using the values of val at the two
children, labeled E and T. Thus, a portion of the dependency graph for every parse tree in which
this production is used looks like Fig. 5.6. As a convention, we shall show the
parse tree edges as dotted lines, while the edges of the dependency graph are
solid.
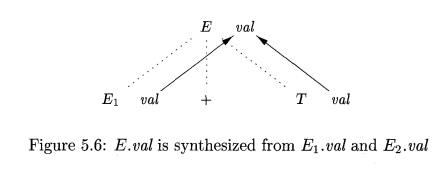
Example
5.5 : An example of a complete dependency graph appears in Fig. 5.7. The nodes
of the dependency graph, represented by the numbers 1 through 9, correspond to
the attributes in the annotated parse tree in Fig. 5.5.
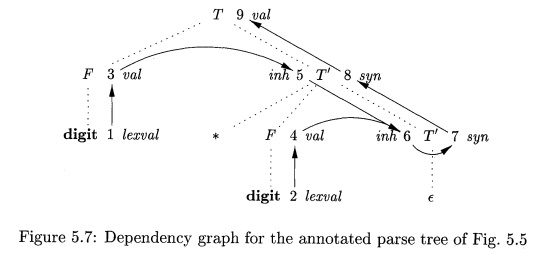
Nodes 1 and 2 represent the attribute lexval associated with the two leaves labeled digit . Nodes 3 and 4
represent the attribute val
associated with the two nodes labeled F.
The edges to node 3 from 1 and to node 4 from 2 result from the semantic rule
that defines F.val in terms of
digit.lexval In fact, F.val equals digit
.lexval, but the edge represents dependence, not equality.
Nodes 5 and 6 represent the inherited attribute T'.inh associated with
each of the occurrences of nonterminal T'. The edge to 5 from 3 is due to the
rule T'.inh = F.val, which defines
T'.inh at the
right child of the root from
F.val at the left child. We see
edges to 6 from node 5 for T'.inh and from node 4 for F.val, because these
values are multiplied to evaluate the attribute inh at node 6.
Nodes 7 and 8 represent the synthesized attribute syn associated with
the occurrences of X". The edge to node 7 from 6 is due to the semantic
rule T'.syn = T'.inh associated with production 3 in Fig. 5.4. The edge to node
8 from 7 is due to a semantic rule associated with production 2.
Finally, node 9 represents the attribute T.val. The edge to 9 from 8 is due
to the semantic rule, T.val = T'.syn, associated with production 1.
2. Ordering the Evaluation of
Attributes
The dependency graph characterizes the possible orders in which we can
evalu-ate the attributes at the various nodes of a parse tree. If the dependency
graph has an edge from node M to node N, then the attribute corresponding to M
must be evaluated before the attribute of N. Thus, the only allowable orders of
evaluation are those sequences of nodes N1, N2,... ,Nk such that if there is an
edge of the dependency graph from Ni to Nj, then i < j. Such an ordering
embeds a directed graph into a linear order, and is called a topological sort
of the graph.
If there is any cycle in the graph, then there are no topological sorts;
that is, there is no way to evaluate the SDD on this parse tree. If there are
no cycles, however, then there is always at least one topological sort. To see
why, since there are no cycles, we can surely find a node with no edge
entering. For if there were no such node, we could proceed from predecessor to
predecessor until we came back to some node we had already seen, yielding a
cycle. Make this node the first in the topological order, remove it from the
dependency graph, and repeat the process on the remaining nodes.
E x a m p l e 5 . 6 : The
dependency graph of Fig. 5.7 has no cycles. One topologi-cal sort is the order
in which the nodes have already been numbered: 1,2, ... ,9 . Notice that every
edge of the graph goes from a node to a higher-numbered node, so this order is
surely a topological sort. There are other topological sorts as well, such as
1,3,5,2,4,6,7,8,9 . •
3. S-Attributed Definitions
As mentioned earlier, given an SDD, it is very hard to tell whether
there exist any parse trees whose dependency graphs have cycles. In practice,
translations can be implemented using classes of SDD's that guarantee an
evaluation order, since they do not permit dependency graphs with cycles.
Moreover, the two classes introduced in this section can be implemented
efficiently in connection with top-down or bottom-up parsing.
The first class is defined as follows:
• An SDD is S-attributed if every attribute is synthesized.
E x a m p l e 5 . 7 : The SDD
of Fig. 5.1 is an example of an S-attributed definition. Each attribute, L.val, E.val, T.val, and F.val is synthesized. •
When an SDD is S-attributed, we can evaluate its attributes in any
bottom-up order of the nodes of the parse tree. It is often especially simple
to evaluate the attributes by performing a postorder traversal of the parse
tree and evalu-ating the attributes at a node N when the traversal leaves N
for the last time. That is, we apply the function postorder, defined below, to the root of the parse tree (see also
the box "Preorder and Postorder Traversals" in Section 2.3.4):
postorder(N) {
for ( each child C of N, from the left ) postorder(C);
evaluate the attributes associated with node N;
}
S-attributed definitions can be implemented during bottom-up parsing,
since a bottom-up parse corresponds to a postorder traversal. Specifically,
postorder corresponds exactly to the order in which an LR parser reduces a
production body to its head. This fact will be used in Section 5.4.2 to
evaluate synthesized attributes and store them on the stack during LR parsing,
without creating the tree nodes explicitly.
4. L-Attributed Definitions
The second class of SDD's is called L-attributed
definitions. The idea behind this class is that, between the attributes
associated with a production body, dependency-graph edges can go from left to
right, but not from right to left (hence "L-attributed"). More
precisely, each attribute must be either
1. Synthesized, or
2. Inherited, but with the rules limited as follows. Suppose that there
is a production A -> X1 X2 ....... Xn, and that there is an inherited
attribute Xi.a computed by a rule associated with this production. Then the
rule may use only:
Inherited attributes associated
with the head A.
Either inherited or synthesized
attributes associated with the occurrences of symbols X1, X2,... , X(i-1) located to
the left of Xi.
Inherited or synthesized
attributes associated with this occurrence of Xi itself, but only in such a way
that there are no cycles in a dependency graph formed by the attributes of this
X i .
Example 5.8 : The SDD in Fig. 5.4 is L-attributed. To see why, consider
the semantic rules for inherited attributes, which are repeated here for
convenience:
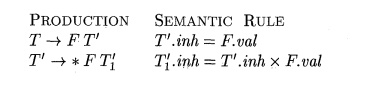
The first of these rules defines the inherited attribute T'.inh using
only F.val, and F appears to the left of T' in the production body, as
required. The second rule defines T[.inh using the inherited attribute T'.inh
associated with the head, and F.val, where F appears to the left of T[ in the
production body.
In each of these cases, the rules use information "from above or
from the left," as required by the class. The remaining attributes are
synthesized. Hence, the SDD is L-attributed. •
Example 5.9 : Any SDD containing the following production and rules
cannot be L-attributed:

The first rule, A.s = B.b, is a legitimate rule in either an
S-attributed or L-attributed SDD. It defines a synthesized attribute A.s in
terms of an attribute at a child (that is, a symbol within the production
body).
The second rule defines an inherited attribute B.i, so the entire SDD
cannot be S-attributed. Further, although the rule is legal, the SDD cannot be
L- attributed, because the attribute C.c is used to help define B.i,
and C is to the right of B in the production body. While attributes at siblings in a parse tree
may be used in L-attributed SDD's, they must be to the left of the symbol whose
attribute is being defined.
5. Semantic Rules with Controlled
Side Effects
In practice, translations involve side effects: a desk calculator might
print a result; a code generator might enter the type of an identifier into a
symbol table. With SDD's, we strike a balance between attribute grammars and
translation schemes. Attribute grammars have no side effects and allow any
evaluation order consistent with the dependency graph. Translation schemes
impose left-to-right evaluation and allow semantic actions to contain any
program fragment; translation schemes are discussed in Section 5.4.
We shall control side effects in SDD's in one of the following ways:
Permit incidental side effects that do not constrain attribute
evaluation. In other words, permit side effects when attribute evaluation based
on any topological sort of the dependency graph produces a "correct"
translation, where "correct" depends on the application.
Constrain the allowable evaluation orders, so that the same translation
is produced for any allowable order. The constraints can be thought of as
implicit edges added to the dependency graph.
As an example of an incidental side effect, let us modify the desk
calculator of Example 5 . 1 to print a result. Instead of the rule L.val =
E.val, which saves the result in the synthesized attribute L.val, consider:

Semantic
Semantic rules that are executed for their side effects, such as
print(E.val), will be treated as the definitions of dummy synthesized
attributes associated with the head of the production. The modified SDD
produces the same translation under any topological sort, since the print statement
is executed at the end, after the result is computed into E.val.
Example 5.10 : The SDD in Fig. 5 . 8 takes a simple declaration D
consisting of a basic type T followed by a list L of identifiers. T can be int
or float. For each identifier on the list, the type is entered into the
symbol-table entry for the identifier. We assume that entering the type for one
identifier does not affect the symbol-table entry for any other identifier.
Thus, entries can be updated in any order. This SDD does not check whether an
identifier is declared more than once; it can be modified to do so.

Nonterminal D represents a
declaration, which, from production 1, consists of a type T followed by a list L of
identifiers. T has one attribute, T.type, which is the type in the
declaration D. Nonterminal L also has one attribute, which we call ink to emphasize that it is an inherited
attribute. The purpose of L.inh is to
pass the declared type down the list of identifiers, so that it can be added to
the appropriate symbol-table entries.
Productions 2 and 3 each evaluate the synthesized attribute T.type,
giving it the appropriate value, integer or float. This type is passed to the
attribute L.inh in the rule for production 1. Production 4 passes L.inh down
the parse tree. That is, the value L1.inh is computed at a parse-tree node by
copying the value of L.inh from the parent of that node; the parent corresponds
to the head of the production.
Productions 4 and 5 also have a rule in which a function addType is
called with two arguments:
id.entry, a lexical value that
points to a symbol-table object, and
L.inh, the type being assigned to
every identifier on the list.
We suppose that function addType
properly installs the type L.inh as the type of the represented
identifier.
A dependency graph for the input
string float idi , i d 2 , i d
3 appears in Fig. 5.9. Numbers 1 through 10 represent the nodes of
the dependency graph.
Nodes 1, 2, and 3 represent the attribute entry associated with each of
the leaves labeled id. Nodes 6, 8, and 10 are the dummy attributes that
represent the application of the function addType to a type and one of these
entry values.
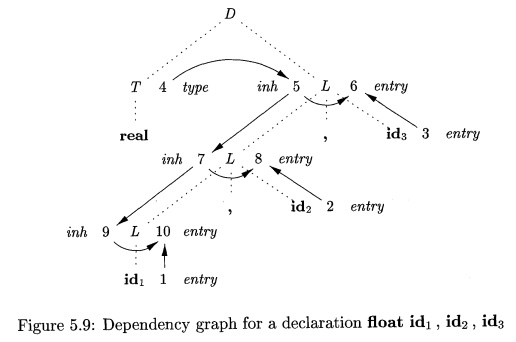
Node 4 represents the attribute T.type,
and is actually where attribute eval-uation begins. This type is then passed to
nodes 5, 7, and 9 representing L.inh
associated with each of the occurrences of the nonterminal L.
6. Exercises for Section 5.2
Exercise 5.2.1 : What are all the topological
sorts for the dependency graph of Fig. 5.7?
Exercise 5 . 2 . 2: For the SDD of Fig. 5.8, give
annotated parse trees for the following expressions:
a) int a, b , c.
b) float w, x, y, z.
Exercise 5.2.3 : Suppose that we have a production A
-> BCD. Each of the four nonterminals A, B, C, and D have two attributes: s
is a synthesized attribute, and i is
an inherited attribute. For each of the sets of rules below, tell whether (i) the rules are consistent with an
S-attributed definition (ii) the
rules are consistent with an L-attributed definition, and (in) whether the rules are consistent with any evaluation order at
all?
a) A.s - B.i + C.s.
b) A.s = B.i + C.s and D.i
= A.i + B.s.
c) A.s - B.s + D.s.
! d) A.s = D.i, B.i =
A.s + C.s, C.i = B.s, and D.i =
B.i + C.i.
Exercise 5 . 2 . 4: This grammar generates binary numbers with a "decimal" point:
S-* L . L | L
L-+LB1B
B -> 0 | 1
Design an L-attributed SDD to compute S.val, the decimal-number value of an input string. For example,
the translation of string 101 . 101 should be the decimal number 5.625. Hint: use an inherited attribute L.side that tells which side of the
decimal point a bit is on.
Exercise 5 . 2 . 5 : Design an S-attributed SDD for
the grammar and translation described
in Exercise 5.2.4.
Exercise 5 . 2 . 6: Implement Algorithm 3.23, which converts a regular expression into a
nondeterministic finite automaton, by an L-attributed SDD on a top-down
parsable grammar. Assume that there is a token char representing any character, and that char.lexval is the character it represents. You may also assume the
existence of a function new() that
returns a new state, that is, a state never before returned by this function.
Use any convenient notation to specify the transitions of the NFA.
Related Topics